A primitive root of a prime 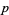 is an integer  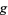such that  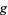(mod 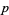) has multiplicative order  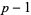(Ribenboim 1996, p. 22). More generally, if  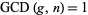( 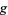and 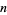 are relatively prime) and  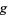is of multiplicative order  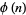modulo  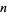where 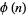 is the totient function, then  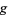is a primitive root of  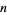(Burton 1989, p. 187). The first definition is a special case of the second since  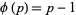for 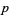 a prime.

A primitive root of a number 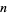 (but not necessarily the smallest primitive root for composite 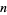) can be computed in the Wolfram Language using PrimitiveRoot[n].

If 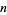 has a primitive root, then it has exactly  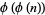of them (Burton 1989, p. 188), which means that if  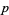is a prime number, then there are exactly  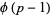incongruent primitive roots of  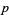(Burton 1989). For 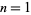, 2, ..., the first few values of  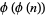are 1, 1, 1, 1, 2, 1, 2, 2, 2, 2, 4, 2, 4, 2, 4, 4, 8, ... (OEIS A010554).  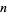has a primitive root if it is of the form 2, 4, 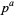, or 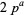, where  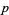is an odd prime and  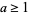(Burton 1989, p. 204). The first few  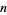for which primitive roots exist are 2, 3, 4, 5, 6, 7, 9, 10, 11, 13, 14, 17, 18, 19, 22, ... (OEIS A033948), so the number of primitive root of orde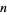r  for 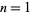, 2, ... are 0, 1, 1, 1, 2, 1, 2, 0, 2, 2, 4, 0, 4, ... (OEIS A046144).

The smallest primitive roots for the first few primes 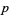 are 1, 2, 2, 3, 2, 2, 3, 2, 5, 2, 3, 2, 6, 3, 5, 2, 2, 2, ... (OEIS A001918). Here is table of the primitive roots for the first few  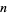for which a primitive root exists (OEIS A046147).

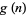2	1
3	2
4	3
5	2, 3
6	5
7	3, 5
9	2, 5
10	3, 7
11	2, 6, 7, 8
13	2, 6, 7, 11

The largest primitive roots for 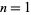, 2, ..., are 0, 1, 2, 3, 3, 5, 5, 0, 5, 7, 8, 0, 11, ... (OEIS A046146). The smallest primitive roots for the first few integers  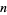are given in the following table (OEIS A046145), which omits  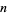when 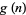 does not exist.

Let 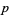 be any odd prime 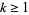, and let

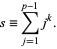(1)

Then

{-1 (mod p) for p-1|k; 0 (mod p) for p-1k " src="http://mathworld.wolfram.com/images/equations/PrimitiveRoot/NumberedEquation2.gif" style="height:44px; width:184px" />

(2)

(Ribenboim 1996, pp. 22-23). For numbers 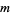 with primitive roots, all  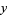satisfying  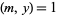are representable as

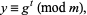(3)

where 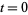, 1, ..., 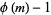,  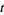is known as the index, and  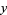is an integer. Kearnes (1984) showed that for any positive integer 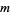, there exist infinitely many primes  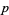such that

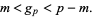(4)

Call the least primitive root 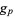. Burgess (1962) proved that

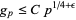(5)

for 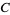 and 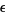 positive constants and  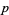sufficiently large (Ribenboim 1996, p. 24).

Matthews (1976) obtained a formula for the "two-dimensional" Artin's constants for the set of primes for which 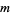 and 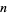 are both primitive roots.

REFERENCES:

Abramowitz, M. and Stegun, I. A. (Eds.). "Primitive Roots." §24.3.4 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 827, 1972.

Burgess, D. A. "On Character Sums and 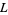-Series." Proc. London Math. Soc. 12, 193-206, 1962.

Burton, D. M. "The Order of an Integer Modulo 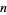," "Primitive Roots for Primes," and "Composite Numbers Having Primitive Roots." §8.1-8.3 in Elementary Number Theory, 4th ed. Dubuque, IA: William C. Brown Publishers, pp. 184-205, 1989.

Guy, R. K. "Primitive Roots." §F9 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 248-249, 1994.

Jones, G. A. and Jones, J. M. "Primitive Roots." §6.2 in Elementary Number Theory. Berlin: Springer-Verlag, pp. 99-103, 1998.

Kearnes, K. "Solution of Problem 6420." Amer. Math. Monthly 91, 521, 1984.

Lehmer, D. H. "A Note on Primitive Roots." Scripta Math. 26, 117-119, 1961.

Matthews, K. R. "A Generalization of Artin's Conjecture for Primitive Roots." Acta Arith. 29, 113-146, 1976.

Nagell, T. "Moduli Having Primitive Roots." §32 in Introduction to Number Theory. New York: Wiley, pp. 107-111, 1951.

Ribenboim, P. The New Book of Prime Number Records. New York: Springer-Verlag, pp. 22-25, 1996.

Riesel, H. Prime Numbers and Computer Methods for Factorization, 2nd ed. Boston, MA: Birkhäuser, p. 97, 1994.

Sloane, N. J. A. Sequences A001918/M0242, A010554, and A033948 in "The On-Line Encyclopedia of Integer Sequences."

Western, A. E. and Miller, J. C. P. Tables of Indices and Primitive Roots. Cambridge, England: Cambridge University Press, pp. xxxvii-xlii, 1968.

اخر الاخبار

اخبار العتبة العباسية المقدسة

المجمَع العلمي يقيم مسابقة الكوثر الخاصة بترتيل القرآن الكريم في كربلاء

قسم الشؤون الفكرية والثقافية يُصدر العدد الثالث والعشرين من مجلّة (أوراق معرفية)

قسم التربية والتعليم يُطلق الموسم التدريبيّ الصيفيّ لملاكات مجموعة العميد التربوية

المجمَع العلمي يُطلق المرحلة الثالثة من مشروع أمير القرّاء الوطني

المزيد

الآخبار الصحية

اختراق علمي.. دواء يؤخر ظهور السكري من النوع الأول لسنوات

هذا ما يحدث لجسمك إن أهملت نظافة فراشك

لماذا تعتبر النساء أكثر عرضة للإصابة بألزهايمر من الرجال؟

لماذا يحذر الخبراء من الإفراط في تناول الفراولة؟

المزيد

الآخبار التكنلوجية

السيارات الكهربائية أنظف بنسبة 73% من سيارات الوقود

سيارة لوسِد الكهربائية تدخل "غينيس" بأطول مدى في العالم

نظرية جديدة تنسف كل ما نعرفه عن تشكل أول قارة في الأرض

منذ 37 ألف عام.. دراسة تكشف "أقدم أمراض" أصابت البشر

المزيد