

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Partition Function P Congruences
المؤلف:
Andrews, G. E. and Garvan, F. G
المصدر:
"Dyson,s Crank of a Partition." Bull. Amer. Math. Soc. 18
الجزء والصفحة:
...
13-1-2020
2901
Partition Function P Congruences

The fraction of odd values of the partition function P(n) is roughly 50%, independent of 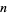 , whereas odd values of
, whereas odd values of 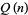 occur with ever decreasing frequency as
occur with ever decreasing frequency as 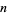 becomes large. Kolberg (1959) proved that there are infinitely many even and odd values of
becomes large. Kolberg (1959) proved that there are infinitely many even and odd values of 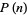 .
.
Leibniz noted that 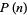 is prime for
is prime for 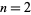 , 3, 4, 5, 6, but not 7. In fact, values of
, 3, 4, 5, 6, but not 7. In fact, values of 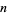 for which
for which 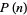 is prime are 2, 3, 4, 5, 6, 13, 36, 77, 132, 157, 168, 186, ... (OEIS A046063), corresponding to 2, 3, 5, 7, 11, 101, 17977, 10619863, ... (OEIS A049575). Numbers which cannot be written as a product of
is prime are 2, 3, 4, 5, 6, 13, 36, 77, 132, 157, 168, 186, ... (OEIS A046063), corresponding to 2, 3, 5, 7, 11, 101, 17977, 10619863, ... (OEIS A049575). Numbers which cannot be written as a product of 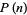 are 13, 17, 19, 23, 26, 29, 31, 34, 37, 38, 39, ... (OEIS A046064), corresponding to numbers of nonisomorphic Abelian groups which are not possible for any group order.
are 13, 17, 19, 23, 26, 29, 31, 34, 37, 38, 39, ... (OEIS A046064), corresponding to numbers of nonisomorphic Abelian groups which are not possible for any group order.
Ramanujan conjectured a number of amazing and unexpected congruences involving 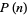 . In particular, he proved
. In particular, he proved
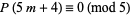 |
(1) |
using Ramanujan's identity (Darling 1919; Hardy and Wright 1979; Drost 1997; Hardy 1999, pp. 87-88; Hirschhorn 1999). Ramanujan (1919) also showed that
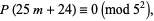 |
(2) |
and Krečmar (1933) proved that
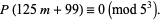 |
(3) |
Watson (1938) then proved the general congruence
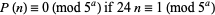 |
(4) |
(Gordon and Hughes 1981; Hardy 1999, p. 89). For 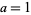 , 2, ..., the corresponding minimal values of
, 2, ..., the corresponding minimal values of 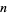 are 4, 24, 99, 599, 2474, 14974, 61849, ... (OEIS A052463). However, the even more general congruences
are 4, 24, 99, 599, 2474, 14974, 61849, ... (OEIS A052463). However, the even more general congruences
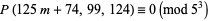 |
(5) |
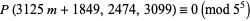 |
(6) |
seem also to hold.
Ramanujan showed that
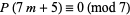 |
(7) |
(Darling 1919), which can be derived using the Euler identity and Jacobi triple product (Hardy 1999, pp. 87-88), and also that
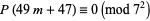 |
(8) |
(Hardy 1999, p. 90). He conjectured that in general
![P(n)=0 (mod 7^b) if 24n=1 (mod 7^b) [incorrect]](http://mathworld.wolfram.com/images/equations/PartitionFunctionPCongruences/NumberedEquation9.gif) |
(9) |
(Gordon and Hughes 1981, Hardy 1999), although Gupta (1936) showed that this is false when 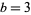 . Watson (1938) subsequently formulated and proved the modified relation
. Watson (1938) subsequently formulated and proved the modified relation
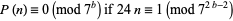 |
(10) |
for 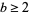 . For
. For 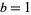 , 2, ..., the corresponding minimal values of
, 2, ..., the corresponding minimal values of 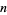 are 0, 47, 2301, 112747, ... (OEIS A052464). However, the even more general congruences
are 0, 47, 2301, 112747, ... (OEIS A052464). However, the even more general congruences
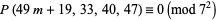 |
(11) |
appear to hold.
Ramanujan showed that
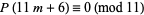 |
(12) |
holds (Gordon and Hughes 1981; Hardy 1999, pp. 87-88), and conjectured the general relation
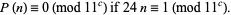 |
(13) |
This was finally proved by Atkin (1967). For 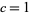 , 2, ..., the corresponding minimal values of
, 2, ..., the corresponding minimal values of 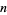 are 6, 116, 721, 14031, ... (OEIS A052465).
are 6, 116, 721, 14031, ... (OEIS A052465).
Atkin and O'Brien (1967) proved
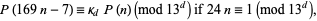 |
(14) |
where 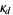 is an integer depending only on
is an integer depending only on 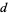 (Gordon and Hughes 1981). For
(Gordon and Hughes 1981). For 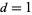 , 2, ..., the corresponding minimal values of
, 2, ..., the corresponding minimal values of 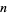 are 6, 162, 1007, 27371, ... (OEIS A052466).
are 6, 162, 1007, 27371, ... (OEIS A052466).
Subbarao (1966) conjectured that in every arithmetic progression 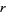 (mod
(mod 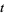 ), there are infinitely many integers
), there are infinitely many integers 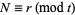 for which
for which 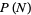 is even, and infinitely many integer
is even, and infinitely many integer 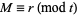 for which
for which 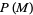 is odd.
is odd.
Dyson (1944) explained congruences modulo 5 and 7 via a mathematical tool he termed a "rank" and conjectured that this approach could be extended to other moduli. The conjecture (sometimes known as the "crank conjecture") was extended to congruences modulo 11 (Andrews and Garvan 1988). Mahlburg (2005) subsequently completely resolved the conjecture with an elegant proof described by Dyson as "beautiful and totally unexpected."
In the Season 4 opening episode "Trust Metric" (2007) of the television crime drama NUMB3RS, math genius Charlie Eppes closes the opening scene by informing his class they will cover partition congruences in the next class (despite the strange fact that the current lesson was on Nash equilibria).
REFERENCES:
Andrews, G. E. and Garvan, F. G. "Dyson's Crank of a Partition." Bull. Amer. Math. Soc. 18, 167-171, 1988.
Atkin, A. O. L. "Proof of a Conjecture of Ramanujan." Glasgow Math. J. 8, 14-32, 1967.
Atkin, A. O. L. and O'Brien, J. N. "Some Properties of 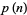 and
and 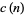 Modulo Powers of 13." Trans. Amer. Math. Soc. 126, 442-459, 1967.
Modulo Powers of 13." Trans. Amer. Math. Soc. 126, 442-459, 1967.
Chowla, S. "Congruence Properties of Partitions." J. London Math. Soc. 9, 247, 1934.
Darling, H. B. C. "On Mr. Ramanujan's Congruence Properties of 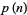 ." Proc. Cambridge Philos. Soc. 19, 217-218, 1919.
." Proc. Cambridge Philos. Soc. 19, 217-218, 1919.
Darling, H. B. C. "Proofs of Certain Identities and Congruences Enunciated by S. Ramanujan." Proc. London Math. Soc. 19, 350-372, 1921.
Drost, J. L. "A Shorter Proof of the Ramanujan Congruence mod 5." Amer. Math. Monthly 104, 963-964, 1997.
Dyson, F. J. Eureka 8, 10-15, 1944.
Dyson, F. J. "Mappings and Symmetries of Partitions." J. Combin. Theory Ser. A 51, 169-180, 1989.
Folsom, A.; Kent, Z. A.;and Ono, K. "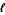 -adic Properties of the Partition Function." www.aimath.org/news/partition/folsom-kent-ono.pdf.
-adic Properties of the Partition Function." www.aimath.org/news/partition/folsom-kent-ono.pdf.
Getz, J. "On Congruence Properties of the Partition Function." Internat. J. Math. Math. Sci. 23, 493-496, 2000.
Gordon, B. and Hughes, K. "Ramanujan Congruences for 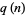 ." In Analytic Number Theory, Proceedings of the Conference Held at Temple University, Philadelphia, Pa., May 12-15, 1980 (Ed. M. I. Knopp). New York: Springer-Verlag, pp. 333-359, 1981.
." In Analytic Number Theory, Proceedings of the Conference Held at Temple University, Philadelphia, Pa., May 12-15, 1980 (Ed. M. I. Knopp). New York: Springer-Verlag, pp. 333-359, 1981.
Gupta, H. "On a Conjecture of Ramanujan." Proc. Indian Acad. Sci. (A) 4, 625-629, 1936.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1999.
Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, 1979.
Hirschhorn, M. D. "Another Short Proof of Ramanujan's Mod 5 Partition Congruences, and More." Amer. Math. Monthly 106, 580-583, 1999.
Kolberg, O. "Note on the Parity of the Partition Function." Math. Scand. 7, 377-378, 1959.
Krečmar, W. "Sur les propriétés de la divisibilité d'une fonction additive." Bull. Acad. Sci. URSS 7, 763-800, 1933.
Lehmer, D. H. "An Application of Schläfli's Modular Equation to a Conjecture of Ramanujan." Bull. Amer. Math. Soc. 44, 84-90, 1938.
Lewis, R. "Relations Between the Rank and the Crank Modulo 9." J. London Math. Soc. 45, 222-231, 1992.
Mahlburg, K. "Partition Congruences and the Andrews-Garvan-Dyson Crank." Proc. National Acad. Sci. USA 102, 15373-15376, 2005.
McKee, M. "Classic Maths Puzzle Cracked at Last." Mar. 21, 2005. http://www.newscientist.com/article.ns?id=dn7180.
Mordell, L. J. "Note on Certain Modular Relations Considered by Messrs Ramanujan, Darling and Rogers." Proc. London Math. Soc. 20, 408-416, 1922.
Ono, K. "Parity of the Partition Function in Arithmetic Progressions." J. reine. angew. Math. 472, 1-15, 1996.
Ono, K. "The Partition Function in Arithmetic Progressions." Math. Ann. 312, 251-260, 1998.
Ono, K. "Distribution of the Partition Function Modulo 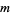 ." Ann. Math. 151, 293-307, 2000.
." Ann. Math. 151, 293-307, 2000.
Ramanujan, S. "Some Properties of 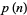 , the Number of Partitions of
, the Number of Partitions of 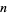 ." Proc. Cambridge Philos. Soc. 19, 207-210, 1919.
." Proc. Cambridge Philos. Soc. 19, 207-210, 1919.
Ramanujan, S. "Congruence Properties of Partitions." Math. Z. 9, 147-153, 1921.
Sloane, N. J. A. Sequences A046063, A046064, A049575, A052462, A052463, A052464, A052465, and A052466 in "The On-Line Encyclopedia of Integer Sequences."
Subbarao, M. V. "Some Remarks on the Partition Function." Amer. Math. Monthly 73, 851-854, 1966.
Watson, G. N. "Ramanujans Vermutung über Zerfällungsanzahlen." J. für Math. 179, 97-128, 1938.
Winquist, L. "An Elementary Proof of 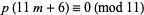 ." J. Combin. Th. 6, 56-59, 1969.
." J. Combin. Th. 6, 56-59, 1969.
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















