A modulo multiplication group is a finite group 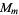 of residue classes prime to  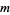under multiplication mod 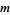.  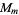is Abelian of group order 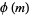, where  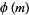is the totient function.

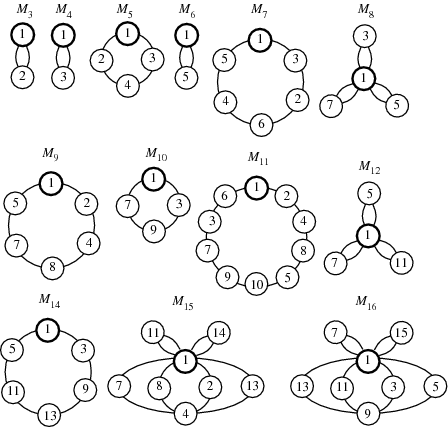
A modulo multiplication group can be visualized by constructing its cycle graph. Cycle graphs are illustrated above for some low-order modulo multiplication groups. Such graphs are constructed by drawing labeled nodes, one for each element  of the residue class, and connecting cycles obtained by iterating 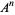. Each edge of such a graph is bidirected, but they are commonly drawn using undirected edges with double edges used to indicate cycles of length two (Shanks 1993, pp. 85 and 87-92).

The following table gives the modulo multiplication groups of small orders, together with their isomorphisms with respect to cyclic groups .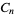

	group		elements
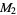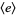		2	1
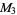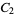		2	1, 2
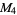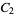		2	1, 3
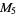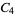		4	1, 2, 3, 4
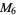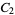		2	1, 5
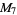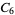		6	1, 2, 3, 4, 5, 6
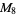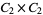		4	1, 3, 5, 7
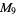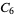		6	1, 2, 4, 5, 7, 8
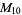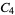		4	1, 3, 7, 9
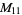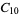		10	1, 2, 3, 4, 5, 6, 7, 8, 9, 10
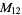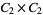		4	1, 5, 7, 11
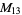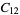		12	1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12
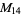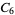		6	1, 3, 5, 9, 11, 13
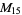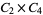		8	1, 2, 4, 7, 8, 11, 13, 14
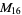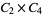		8	1, 3, 5, 7, 9, 11, 13, 15
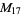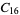		16	1, 2, 3, ..., 16
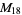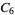		6	1, 5, 7, 11, 13, 17
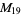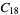		18	1, 2, 3, ..., 18
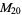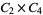		8	1, 3, 7, 9, 11, 13, 17, 19
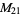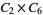		12	1, 2, 4, 5, 8, 10, 11, 13, 16, 17, 19, 20
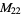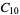		10	1, 3, 5, 7, 9, 13, 15, 17, 19, 21
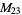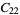		22	1, 2, 3, ..., 22
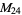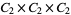		8	1, 5, 7, 11, 13, 17, 19, 23

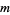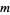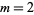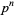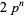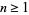 is a cyclic group (which occurs exactly when  has a primitive root) iff  is of one of the forms , 4, , or , where  is an odd prime and  (Shanks 1993, p. 92). The first few of these are 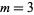, 4, 5, 6, 7, 9, 10, 11, 13, 14, 17, 18, 19, ... (OEIS A033948; Shanks 1993, p. 84).

The only ordered 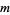 for which the elements of  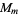are all self-conjugate are the divisors of 24: 1, 2, 3, 4, 6, 8, 12, 24 (OEIS A018253; Eggar 2000). These correspond to the groups 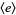, , 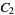, 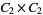and 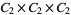. This also means that no modulo multiplication group is isomorphic to a direct product of more than three copies of .

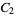Isomorphic modulo multiplication groups can be determined using a particular type of factorization of the totient function 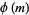 using the property that

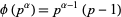(1)

as described by Shanks (1993, pp. 92-93). To perform this factorization, begin by analogy with computation of the totient function by factoring 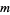 in the standard form

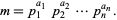(2)

Now for each power of an odd prime, write

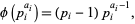(3)

and factor the leading term

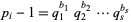(4)

as

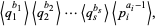(5)

where 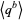 denotes the explicit expansion of  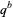(i.e., 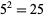), and the last term is omitted if  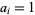(since in that case, ).

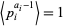If 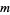 contains a power of 2 so that 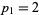, then write

{nothing for a_1<2; <2> for a_1=2; <2><2^(a_1-2)> for a_1>2. " src="http://mathworld.wolfram.com/images/equations/ModuloMultiplicationGroup/NumberedEquation6.gif" style="height:68px; width:201px" />

(6)

Now combine terms from the odd and even primes, write them as a product and combine any unambiguous products of terms. The resulting expression is denoted 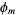 and the group  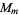is isomorphic to a direct product of cyclic groups of orders given by .

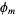For example, consider the modulo multiplication group of order 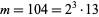. The only odd prime factor is 13, so factoring gives 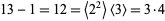. 104 contains a factor of 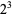, so the rule for even prime factors gives 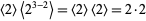. Combining these two gives .

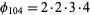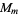 and 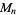 are isomorphic iff  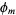and 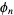 are identical. More specifically, the abstract group corresponding to a given  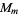can be determined explicitly in terms of a group direct product of cyclic groups of the so-called characteristic factors, whose product is denoted 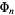. This representation is obtained from  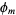as the set of products of largest powers of each factor of 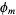. For example, for 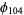, the largest power of 2 is  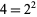and the largest power of 3 is 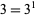, so the first characteristic factor is 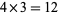, leaving  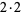(i.e., only powers of two). The largest power remaining is 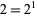, so the second characteristic factor is 2, leaving 2, which is the third and last characteristic factor. Therefore, 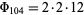, and the group  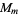is isomorphic to .

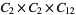The following table summarizes the isomorphic modulo multiplication groups 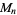 for the first few  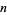and identifies the corresponding abstract group. No  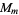is isomorphic to the cyclic group 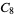, quaternion group 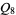, or the dihedral group 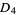. However, every finite Abelian group is isomorphic to a subgroup of  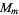for infinitely many different values of  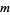(Shanks 1993, p. 96). Cycle graphs corresponding to  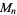for small  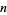are illustrated above, and more complicated cycle graphs are illustrated by Shanks (1993, pp. 87-92).

The following table gives the orders of modulo multiplication groups 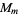 that are isomorphic to direct products of cyclic groups for .

group	isomorphic
	, ,
	,
	,
	, , ,
	, , ,
	,
	,
	, , ,
	,
	,
	, ,
	,
	,
	,
	, ,
	,

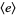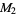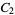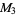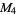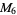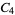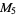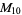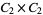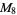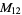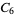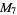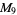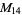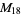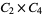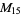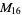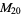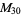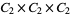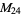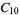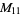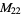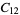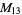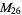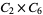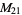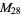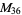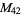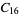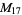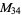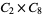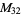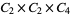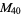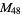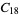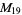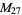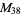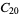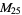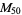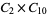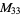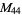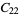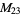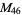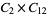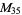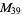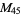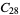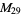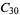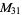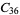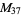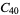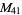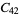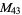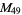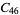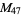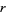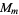The number of characteristic factors  of  for 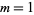, 2, ... are 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 2, ... (OEIS A046072).

The number of quadratic residues in 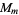 for 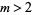 are given by  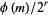(Shanks 1993, p. 95). The first few for 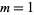, 2, ... are 0, 1, 1, 1, 2, 1, 3, 1, 3, 2, 5, 1, 6, ... (OEIS A046073).

In the table below, 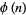 is the totient function (OEIS A000010) factored into characteristic factors,  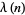is the Carmichael function (OEIS A011773), and  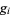are the smallest generators of the group  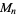(of which there is a number equal to the number of characteristic factors).

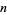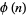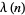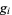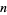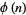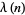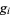3	2	2	2	27	18	18	2
4	2	2	3	28		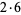6	13, 3
5	4	4	2	29	28	28	2
6	2	2	5	30		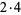4	11, 7
7	6	6	3	31	30	30	3
8		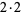2	7, 3	32		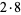8	31, 3
9	6	6	2	33		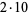10	10, 2
10	4	4	3	34	16	16	3
11	10	10	2	35		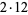12	6, 2
12		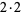2	5, 7	36		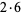6	19,5
13	12	12	2	37	36	36	2
14	6	6	3	38	18	18	3
15		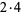4	14, 2	39		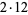12	38, 2
16		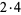4	15, 3	40		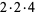4	39, 11, 3
17	16	16	3	41	40	40	6
18	6	6	5	42		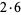6	13, 5
19	18	18	2	43	42	42	3
20		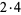4	19, 3	44		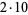10	43, 3
21		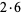6	20, 2	45		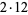12	44, 2
22	10	10	7	46	22	22	5
23	22	22	5	47	46	46	5
24		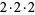2	5, 7, 13	48		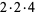4	47, 7, 5
25	20	20	2	49	42	42	3
26	12	12	7	50	20	20	3

REFERENCES:

Eggar, M. H. "A Curious Property of the Integer 24." Math. Gaz. 84, 96-97, March 2000.

Riesel, H. "The Structure of the Group 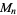." Prime Numbers and Computer Methods for Factorization, 2nd ed. Boston, MA: Birkhäuser, pp. 270-272, 1994.

Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, pp. 61-62 and 92, 1993.

Sloane, N. J. A. Sequences A000010/M0299, A011773, A018253, A033948, A046072, and A046073 in "The On-Line Encyclopedia of Integer Sequences."

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم بين الحرمين يقدم ورشة تدريبية عن صيانة العجلات الكهربائية للملاكات الفنية في مدينة الفردوس

مجموعة مشاتل الكفيل تستقبل طلبة مجموعة العميد التربوية

قسم العلاقات العامة ينظم محاضرة ثقافية لوفد مركز الزهراء (عليها السلام) من ألمانيا

المجمع العلمي يحيي ذكرى ولادة الإمام علي (عليه السلام) في كربلاء

المزيد

الآخبار الصحية

طبيب يكشف أفضل مكمل غذائي لتحسين المزاج ودعم الصحة النفسية

دراسة جديدة تكشف أضرار الأطعمة الجاهزة على القلب ؟

6 أطعمة طبيعية تهدئ الزكام دون أدوية.. تعرف عليهم

ماذا يحدث لأعراض الزكام عند تناول الثوم بانتظام؟

المزيد

الآخبار التكنلوجية

ابتكار ثوري في بطاريات السيارات الكهربائية.. سعة أعلى 4 مرات

ماذا يحدث لجسمك عند شرب الماء الساخن يوميا؟

7 فوائد "خفية" لشرب شاي الكركديه كل يوم

دراسة تكشف قدرة الحيتان على سماع الأصوات منخفضة وعالية التردد من مسافة بعيدة

المزيد