Modular Arithmetic

Modular arithmetic is the arithmetic of congruences, sometimes known informally as "clock arithmetic." In modular arithmetic, numbers "wrap around" upon reaching a given fixed quantity, which is known as the modulus (which would be 12 in the case of hours on a clock, or 60 in the case of minutes or seconds on a clock).

Formally, modular arithmetic is the arithmetic of any nontrivial homomorphic image of the ring of integers. For any such homomorphic image 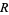 of 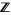, there is an integer  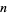such that  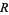is isomorphic to the ring  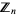of integers modulo 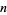. The addition in the ring  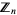is determined from addition in  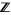by computing the remainder, upon division by 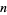, of the sum  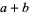of two integers  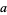and 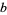. Similarly, for multiplication in the ring 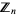, one multiplies two integers  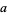and 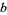, and computes the remainder upon division of  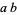by .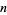

For each positive integer 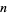, the ring  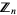has 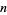 elements, namely the equivalence classes of each of the nonnegative integers less than 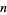, under the equivalence relation  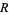that is defined according to the rule  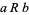iff 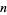 divides 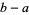. It is natural and common to denote the equivalence class  (under the equivalence relation 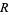) of a nonnegative integer  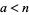by .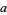

For example, in arithmetic modulo 12 (for which the associated ring is 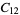), the allowable numbers are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, and 11. This arithmetic is sometimes referred to as "clock arithmetic" because the additive structure here is the same as that used to determine times for a twelve-hour clock, except that 0 is often replaced, on a clock, by 12. Example calculations in arithmetic modulo 12 include statements like "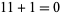", or "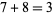", or "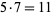," although the equal sign  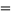is commonly replaced with the congruence sign  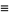in such statements to indicate that modular arithmetic is being used. More explicitly still, a notation such as

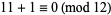is frequently used.

Arithmetic modulo 2 is sometimes referred to as "Boolean arithmetic", because the ring 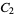 is the canonical example of a Boolean ring.