


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 8-3-2020
Date: 17-12-2019
Date: 12-8-2020
|
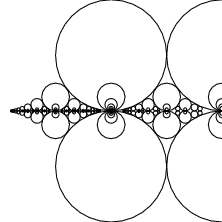
Pick any two relatively prime integers 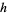 and
and 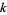 , then the circle
, then the circle 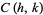 of radius
of radius 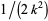 centered at
centered at 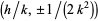 is known as a Ford circle. No matter what and how many
is known as a Ford circle. No matter what and how many 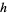 s and
s and 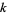 s are picked, none of the Ford circles intersect (and all are tangent to the x-axis). This can be seen by examining the squared distance between the centers of the circles with
s are picked, none of the Ford circles intersect (and all are tangent to the x-axis). This can be seen by examining the squared distance between the centers of the circles with 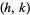 and
and 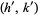 ,
,
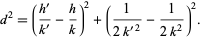 |
(1) |
Let 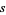 be the sum of the radii
be the sum of the radii
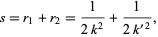 |
(2) |
then
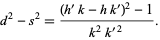 |
(3) |
But 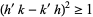 , so
, so 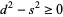 and the distance between circle centers is
and the distance between circle centers is 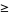 the sum of the circle radii, with equality (and therefore tangency) iff
the sum of the circle radii, with equality (and therefore tangency) iff 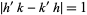 . Ford circles are related to the Farey sequence (Conway and Guy 1996).
. Ford circles are related to the Farey sequence (Conway and Guy 1996).
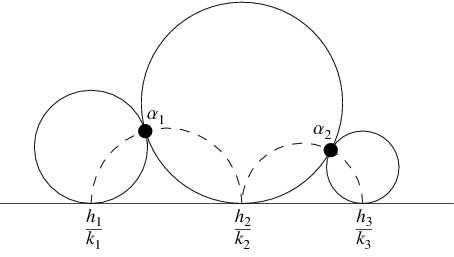
If 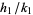 ,
, 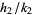 , and
, and 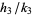 are three consecutive terms in a Farey sequence, then the circles
are three consecutive terms in a Farey sequence, then the circles 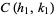 and
and 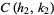 are tangent at
are tangent at
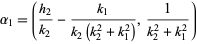 |
(4) |
and the circles 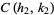 and
and 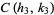 intersect in
intersect in
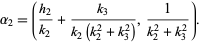 |
(5) |
Moreover, 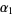 lies on the circumference of the semicircle with diameter
lies on the circumference of the semicircle with diameter 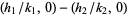 and
and 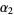 lies on the circumference of the semicircle with diameter
lies on the circumference of the semicircle with diameter 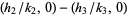 (Apostol 1997, p. 101).
(Apostol 1997, p. 101).
REFERENCES:
Apostol, T. M. "Ford Circles." §5.5 in Modular Functions and Dirichlet Series in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 99-102, 1997.
Conway, J. H. and Guy, R. K. "Farey Fractions and Ford Circles." The Book of Numbers. New York: Springer-Verlag, pp. 152-154, 1996.
Ford, L. R. "Fractions." Amer. Math. Monthly 45, 586-601, 1938.
Pickover, C. A. "Fractal Milkshakes and Infinite Archery." Ch. 14 in Keys to Infinity. New York: W. H. Freeman, pp. 117-125, 1995.
Rademacher, H. Higher Mathematics from an Elementary Point of View. Boston, MA: Birkhäuser, 1983.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|