


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات 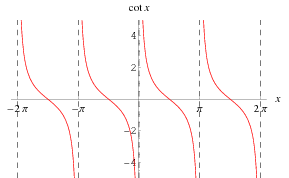
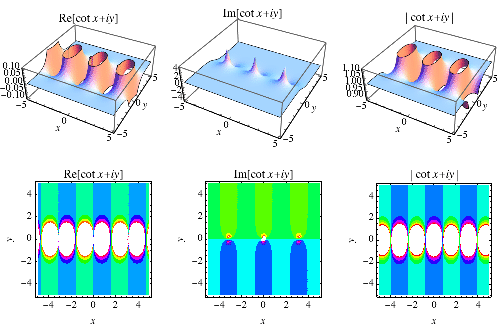 |
The cotangent function 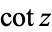 is the function defined by
is the function defined by
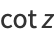 |
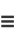 |
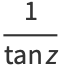 |
(1) |
 |
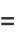 |
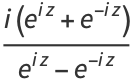 |
(2) |
 |
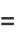 |
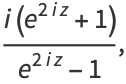 |
(3) |
where 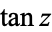 is the tangent. The cotangent is implemented in the Wolfram Language as Cot[z].
is the tangent. The cotangent is implemented in the Wolfram Language as Cot[z].
The notations 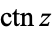 (Erdélyi et al. 1981, p. 7; Jeffrey 2000, p. 111) and
(Erdélyi et al. 1981, p. 7; Jeffrey 2000, p. 111) and 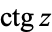 (Gradshteyn and Ryzhik 2000, p. xxix) are sometimes used in place of
(Gradshteyn and Ryzhik 2000, p. xxix) are sometimes used in place of 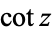 . Note that the cotangent is not in as widespread use in Europe as are
. Note that the cotangent is not in as widespread use in Europe as are 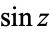 ,
, 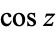 , and
, and 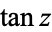 , although it does appear explicitly in various German and Russian handbooks (e.g., Gradshteyn and 2000, p. 28). Interestingly,
, although it does appear explicitly in various German and Russian handbooks (e.g., Gradshteyn and 2000, p. 28). Interestingly, 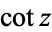 is treated on par with the other trigonometric functions in most tabulations (Gellert et al. 1989, p. 222; Gradshteyn and Ryzhik 2000, p. 28), while
is treated on par with the other trigonometric functions in most tabulations (Gellert et al. 1989, p. 222; Gradshteyn and Ryzhik 2000, p. 28), while 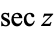 and
and 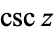 are sometimes not (Gradshteyn and Ryzhik 2000, p. 28).
are sometimes not (Gradshteyn and Ryzhik 2000, p. 28).
An important identity connecting the cotangent with the cosecant is given by
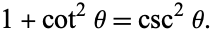 |
(4) |
The cotangent has smallest real fixed point 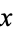 such
such 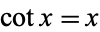 at 0.8603335890... (OEIS A069855; Bertrand 1865, p. 285).
at 0.8603335890... (OEIS A069855; Bertrand 1865, p. 285).
The derivative is given by
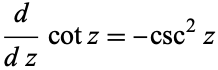 |
(5) |
and the indefinite integral by
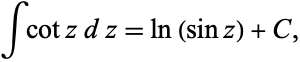 |
(6) |
where 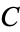 is a constant of integration.
is a constant of integration.
Definite integrals include
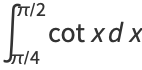 |
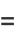 |
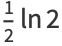 |
(7) |
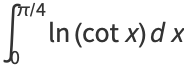 |
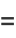 |
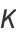 |
(8) |
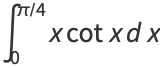 |
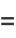 |
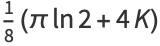 |
(9) |
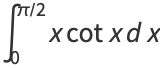 |
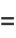 |
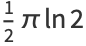 |
(10) |
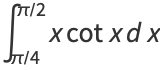 |
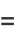 |
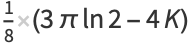 |
(11) |
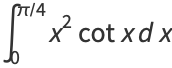 |
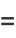 |
![1/(64)[16piK+2pi^2ln2-34zeta(3)]](http://mathworld.wolfram.com/images/equations/Cotangent/Inline41.gif) |
(12) |
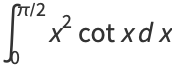 |
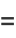 |
![1/8[2pi^2ln2-7zeta(3)],](http://mathworld.wolfram.com/images/equations/Cotangent/Inline44.gif) |
(13) |
where 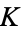 is Catalan's constant,
is Catalan's constant, 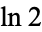 is the natural logarithm of 2, and
is the natural logarithm of 2, and 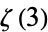 is Apéry's constant. Integrals (9) and (10) were considered by Glaisher (1893). Additional integrals include
is Apéry's constant. Integrals (9) and (10) were considered by Glaisher (1893). Additional integrals include
![int_0^(pi/4)cot^nxdx=1/4[psi_0(1/4(3-n))-psi_0(1/4(1-n))]](http://mathworld.wolfram.com/images/equations/Cotangent/NumberedEquation4.gif) |
(14) |
for ![R[n]<1](http://mathworld.wolfram.com/images/equations/Cotangent/Inline48.gif) , where
, where 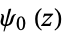 is the digamma function, and
is the digamma function, and
![int_0^(pi/2)cot^nxdx=1/2pisec[1/2(pin)]](http://mathworld.wolfram.com/images/equations/Cotangent/NumberedEquation5.gif) |
(15) |
for ![-1<R[n]<1](http://mathworld.wolfram.com/images/equations/Cotangent/Inline50.gif) .
.
The Laurent series for 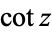 about the origin is
about the origin is
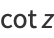 |
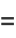 |
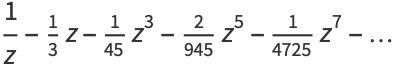 |
(16) |
 |
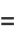 |
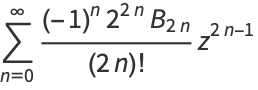 |
(17) |
(OEIS A002431 and A036278), where 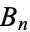 is a Bernoulli number.
is a Bernoulli number.
A nice sum identity for the cotangent is given by
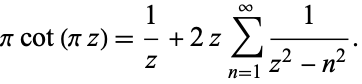 |
(18) |
For an integer 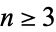 ,
,  is rational only for
is rational only for 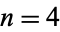 . In particular, the algebraic degrees of
. In particular, the algebraic degrees of  for
for 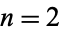 , 3, ... are 1, 2, 1, 4, 2, 6, 2, 6, 4, 10, 2, ... (OEIS A089929).
, 3, ... are 1, 2, 1, 4, 2, 6, 2, 6, 4, 10, 2, ... (OEIS A089929).
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Circular Functions." §4.3 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 71-79, 1972.
Bertrand, J. Exercise II in Traité d'algbre, Vols. 1-2, 4th ed. Paris, France: Librairie de L. Hachette et Cie, p. 285, 1865.
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 215, 1987.
Erdélyi, A.; Magnus, W.; Oberhettinger, F.; and Tricomi, F. G. Higher Transcendental Functions, Vol. 1. New York: Krieger, p. 6, 1981.
Gellert, W.; Gottwald, S.; Hellwich, M.; Kästner, H.; and Künstner, H. (Eds.). VNR Concise Encyclopedia of Mathematics, 2nd ed. New York: Van Nostrand Reinhold, 1989.
Glaisher, J. W. L. "On Certain Numerical Products in which the Exponents Depend Upon the Numbers." Messenger Math. 23, 145-175, 1893.
Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press, 2000.
Jeffrey, A. "Trigonometric Identities." §2.4 in Handbook of Mathematical Formulas and Integrals, 2nd ed. Orlando, FL: Academic Press, pp. 111-117, 2000.
Sloane, N. J. A. Sequences A002431/M0124, A036278, A069855, and A089929 in "The On-Line Encyclopedia of Integer Sequences."
Spanier, J. and Oldham, K. B. "The Tangent 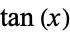 and Cotangent
and Cotangent 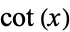 Functions." Ch. 34 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 319-330, 1987.
Functions." Ch. 34 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 319-330, 1987.
Tropfke, J. Teil IB, §2. "Die Begriffe von Tangens und Kotangens eines Winkels." In Geschichte der Elementar-Mathematik in systematischer Darstellung mit besonderer Berücksichtigung der Fachwörter, fünfter Band, zweite aufl. Berlin and Leipzig, Germany: de Gruyter, pp. 23-28, 1923.
Zwillinger, D. (Ed.). "Trigonometric or Circular Functions." §6.1 in CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, pp. 452-460, 1995.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|