Fibonacci Polynomial

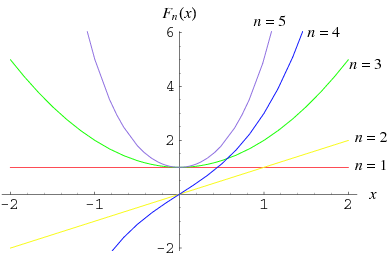
The 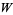 polynomials obtained by setting  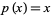and 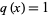 in the Lucas polynomial sequence. (The corresponding  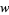polynomials are called Lucas polynomials.) They have explicit formula

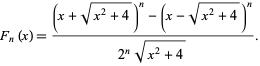(1)

The Fibonacci polynomial 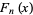 is implemented in the Wolfram Language as Fibonacci[n, x].

The Fibonacci polynomials are defined by the recurrence relation

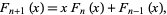(2)

with 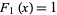 and .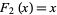

The first few Fibonacci polynomials are

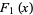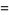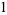			(3)
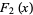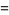			(4)
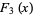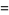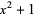			(5)
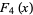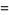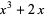			(6)
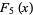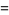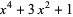			(7)

(OEIS A049310).

The Fibonacci polynomials have generating function

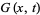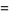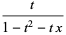			(8)
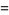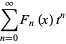			(9)
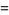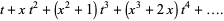			(10)

The Fibonacci polynomials are normalized so that

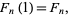(11)

where the 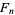s are Fibonacci numbers.

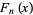 is also given by the explicit sum formula

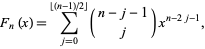(12)

where 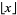 is the floor function and  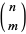is a binomial coefficient.

The derivative of 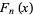 is given by

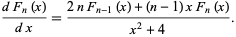(13)

The Fibonacci polynomials have the divisibility property 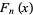 divides  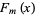iff 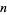 divides 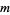. For prime 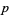,  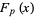is an irreducible polynomial. The zeros of  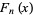are 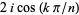 for 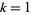, ..., 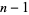. For prime 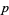, these roots are  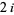times the real part of the roots of the 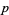th cyclotomic polynomial (Koshy 2001, p. 462).

The identity

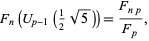(14)

for 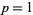, 3, ... and  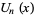a Chebyshev polynomial of the second kind gives the identities

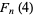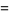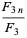			(15)
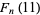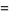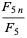			(16)
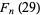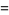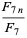			(17)
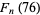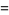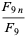			(18)

and so on, where 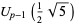 gives the sequence 4, 11, 29, ... (OEIS A002878).

The Fibonacci polynomials are related to the Morgan-Voyce polynomials by

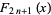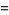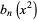			(19)
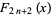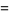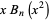			(20)

(Swamy 1968).

REFERENCES:

Koshy, T. Fibonacci and Lucas Numbers with Applications. New York: Wiley, 2001.

Sloane, N. J. A. Sequence A002878/M3420 in "The On-Line Encyclopedia of Integer Sequences."

Swamy, M. N. S. "Further Properties of Morgan-Voyce Polynomials." Fib. Quart. 6, 167-175, 1968.