
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 25-4-2018
Date: 21-8-2018
Date: 16-5-2018
|
Polynomials 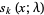 which form a Sheffer sequence with
which form a Sheffer sequence with
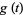 |
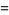 |
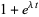 |
(1) |
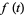 |
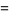 |
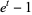 |
(2) |
and have generating function
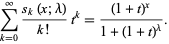 |
(3) |
The first few are
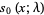 |
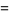 |
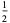 |
(4) |
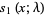 |
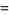 |
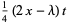 |
(5) |
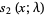 |
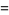 |
![1/4[2x(x-lambda-1)+lambda].](http://mathworld.wolfram.com/images/equations/BoolePolynomial/Inline16.gif) |
(6) |
Jordan (1965) considers the related polynomials 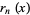 which form a Sheffer sequence with
which form a Sheffer sequence with
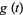 |
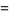 |
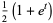 |
(7) |
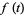 |
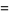 |
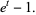 |
(8) |
These polynomials have generating function
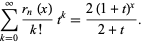 |
(9) |
The first few are
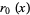 |
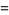 |
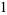 |
(10) |
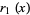 |
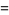 |
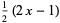 |
(11) |
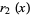 |
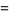 |
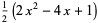 |
(12) |
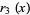 |
 |
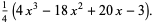 |
(13) |
The Peters polynomials are a generalization of the Boole polynomials.
REFERENCES:
Boas, R. P. and Buck, R. C. Polynomial Expansions of Analytic Functions, 2nd print., corr. New York: Academic Press, p. 37, 1964.
Jordan, C. Calculus of Finite Differences, 3rd ed. New York: Chelsea, 1965.
Roman, S. The Umbral Calculus. New York: Academic Press, 1984.



|
|
|
|
لخفض ضغط الدم.. دراسة تحدد "تمارين مهمة"
|
|
|
|
|
|
|
طال انتظارها.. ميزة جديدة من "واتساب" تعزز الخصوصية
|
|
|
|
|
|
|
مشاتل الكفيل تزيّن مجمّع أبي الفضل العبّاس (عليه السلام) بالورد استعدادًا لحفل التخرج المركزي
|
|
|