


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 10-8-2019
Date: 9-10-2019
Date: 20-8-2018
|
The first Göllnitz-Gordon identity states that the number of partitions of 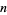 in which the minimal difference between parts is at least 2, and at least 4 between even parts, equals the number of partitions of
in which the minimal difference between parts is at least 2, and at least 4 between even parts, equals the number of partitions of 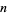 into parts congruent to 1, 4, or 7 (mod 8). For example, taking
into parts congruent to 1, 4, or 7 (mod 8). For example, taking 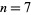 , the resulting two sets of partitions are
, the resulting two sets of partitions are 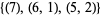 and
and 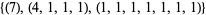 .
.
The second Göllnitz-Gordon identity states that the number of partitions of 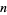 in which the minimal difference between parts is at least 2, the minimal difference between even parts is at least 4, and all parts are greater than 2, equals the number of partitions of
in which the minimal difference between parts is at least 2, the minimal difference between even parts is at least 4, and all parts are greater than 2, equals the number of partitions of 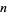 into parts congruent to 3, 4, or 5 (mod 8). For example, taking
into parts congruent to 3, 4, or 5 (mod 8). For example, taking 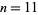 , the resulting two sets of partitions are
, the resulting two sets of partitions are 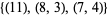 and
and 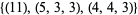 .
.
The Göllnitz-Gordon identities are due to H. Göllnitz and were included in his 1961 unpublished honors baccalaureate thesis. However, essentially no one knew about the results until Gordon (1965) independently rediscovered them.
The analytic counterparts of the Göllnitz-Gordon partition identities are the q-series identities
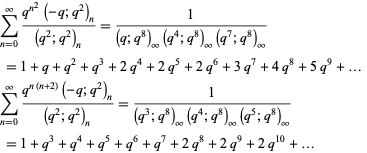 |
(OEIS A036016 and A036015), where 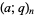 denotes a q-series and the coefficients give the number of partitions satisfying the corresponding Göllnitz-Gordon identity.
denotes a q-series and the coefficients give the number of partitions satisfying the corresponding Göllnitz-Gordon identity.
These analytic identities were published by Slater (1952) and predate the partition theorem by a decade. Equation (◇) is number 36 and equation (◇) is number 34 in Slater's list. However, it has recently been discovered by A. Sills that two analytic identities equivalent to the analytic Göllnitz-Gordon identities were recorded by Ramanujan in his lost notebook, and thus that Ramanujan knew these identities more than 30 years before Slater rediscovered them (Andrews and Berndt 2008, p. 37)!
REFERENCES:
Andrews, G. E. On the General Rogers-Ramanujan Theorem. Providence, RI: Amer. Math. Soc., 1974.
Andrews, G. E. The Theory of Partitions. Cambridge, England: Cambridge University Press, p. 114, 1998.
Andrews, G. E. and Berndt, B. C. Ramanujan's Lost Notebook, Part II. New York: Springer, 2008.
Göllnitz, H. "Partitionen mit Differenzenbedingungen." J. reine angew. Math. 225, 154-190, 1967.
Gordon, B. "Some Continued Fractions of the Rogers-Ramanujan Type." Duke Math. J. 32, 741-748, 1965.
Gordon, B. and McIntosh, R. J. "Some Eighth Order Mock Theta Functions." J. London Math. Soc. 62, 321-335, 2000.
Mc Laughlin, J.; Sills, A. V.; and Zimmer, P. "Dynamic Survey DS15: Rogers-Ramanujan-Slater Type Identities." Electronic J. Combinatorics, DS15, 1-59, May 31, 2008. http://www.combinatorics.org/Surveys/ds15.pdf.
Selberg, A. "Über die Mock-Thetafunktionen siebenter Ordnung." Arch. Math. og Naturvidenskab 41, 3-15, 1938.
Slater, L. J. "Further Identities of the Rogers-Ramanujan Type." Proc. London Math. Soc. Ser. 2 54, 147-167, 1952.
Sloane, N. J. A. Sequences A036015 and A036016 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|