Elementary Function

A function built up of a finite combination of constant functions, field operations (addition, multiplication, division, and root extractions--the elementary operations)--and algebraic, exponential, and logarithmic functions and their inverses under repeated compositions (Shanks 1993, p. 145; Chow 1999). Among the simplest elementary functions are the logarithm, exponential function (including the hyperbolic functions), power function, and trigonometric functions.

Following Liouville (1837, 1838, 1839), Watson (1966, p. 111) defines the elementary transcendental functions as

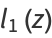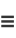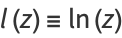			(1)
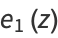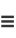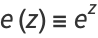			(2)
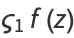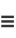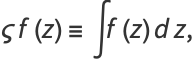			(3)

and lets 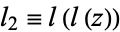, etc.

Not all functions are elementary. For example, the normal distribution function

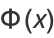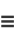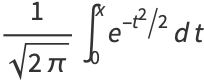			(4)
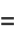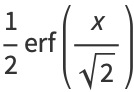			(5)

is a notorious example of a nonelementary function, where 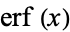 is erf (sometimes known as the error function). The elliptic integral

(6)

is another, where 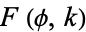 is an elliptic integral of the first kind.

REFERENCES:

Bronstein, M. Symbolic Integration I: Transcendental Functions. New York: Springer-Verlag, 1997.

Chow, T. Y. "What is a Closed-Form Number." Amer. Math. Monthly 106, 440-448, 1999.

Geddes, K. O.; Czapor, S. R.; and Labahn, G. "Elementary Functions." §12.2 in Algorithms for Computer Algebra. Amsterdam, Netherlands: Kluwer, pp. 512-519, 1992.

Hardy, G. H. Orders of Infinity: The 'infinitarcalcul' of Paul Du Bois-Reymond, 2nd ed. Cambridge, England: Cambridge University Press, 1924.

Knopp, K. "The Elementary Functions." §23 in Theory of Functions Parts I and II, Two Volumes Bound as One, Part I. New York: Dover, pp. 96-98, 1996.

Liouville, J. "Sur la classification des Transcendantes et sur l'impossibilité d'exprimer les racines des certaines équations en fonction finie explicite des coefficients. Part 1." J. Math. pure appl. 2, 56-105, 1837.

Liouville, J. "Sur la classification des Transcendantes et sur l'impossibilité d'exprimer les racines des certaines équations en fonction finie explicite des coefficients. Part 2." J. Math. pure appl. 3, 523-547, 1838.

Liouville, J. "Sur l'integration d'une classe d'Équations différentielles du second ordre en quantités finies explicites." J. Math. pure appl. 4, 423-456, 1839.

Marchisotto, E. A. and Zakeri, G.-A. "An Invitation to Integration in Finite Terms." College Math. J. 25, 295-308, 1994.

Ritt, J. F. "Elementary Functions and Their Inverses." Trans. Amer. Math. Soc. 27, 68-90, 1925.

Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, 1993.

Trott, M. "Elementary Transcendental Functions." §2.2.3 in The Mathematica GuideBook for Programming. New York: Springer-Verlag, pp. 164-171, 2004. http://www.mathematicaguidebooks.org/.

Watson, G. N. A Treatise on the Theory of Bessel Functions, 2nd ed. Cambridge, England: Cambridge University Press, p. 111, 1966.

Zoładek, H. "Two Remarks About Picard-Vessiot Extensions and Elementary Functions. Dedicated to the Memory of Anzelm Iwanik." Colloq. Math. 84/85, 173-183, 2000.