


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 30-7-2019
Date: 2-10-2019
Date: 12-8-2018
|
The delta function is a generalized function that can be defined as the limit of a class of delta sequences. The delta function is sometimes called "Dirac's delta function" or the "impulse symbol" (Bracewell 1999). It is implemented in the Wolfram Language as DiracDelta[x].
Formally, 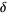 is a linear functional from a space (commonly taken as a Schwartz space
is a linear functional from a space (commonly taken as a Schwartz space 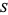 or the space of all smooth functions of compact support
or the space of all smooth functions of compact support 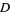 ) of test functions
) of test functions 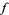 . The action of
. The action of 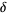 on
on 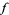 , commonly denoted
, commonly denoted ![delta[f]](http://mathworld.wolfram.com/images/equations/DeltaFunction/Inline7.gif) or
or 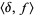 , then gives the value at 0 of
, then gives the value at 0 of 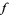 for any function
for any function 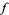 . In engineering contexts, the functional nature of the delta function is often suppressed.
. In engineering contexts, the functional nature of the delta function is often suppressed.
The delta function can be viewed as the derivative of the Heaviside step function,
![d/(dx)[H(x)]=delta(x)](http://mathworld.wolfram.com/images/equations/DeltaFunction/NumberedEquation1.gif) |
(1) |
(Bracewell 1999, p. 94).
The delta function has the fundamental property that
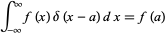 |
(2) |
and, in fact,
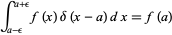 |
(3) |
for 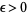 .
.
Additional identities include
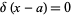 |
(4) |
for 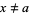 , as well as
, as well as
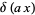 |
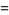 |
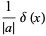 |
(5) |
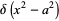 |
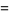 |
![1/(2|a|)[delta(x+a)+delta(x-a)]](http://mathworld.wolfram.com/images/equations/DeltaFunction/Inline18.gif) |
(6) |
More generally, the delta function of a function of  is given by
is given by
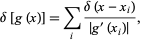 |
(7) |
where the 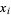 s are the roots of
s are the roots of 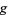 . For example, examine
. For example, examine
![delta(x^2+x-2)=delta[(x-1)(x+2)].](http://mathworld.wolfram.com/images/equations/DeltaFunction/NumberedEquation6.gif) |
(8) |
Then 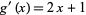 , so
, so 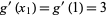 and
and 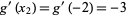 , giving
, giving
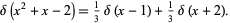 |
(9) |
The fundamental equation that defines derivatives of the delta function 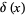 is
is
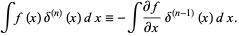 |
(10) |
Letting 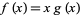 in this definition, it follows that
in this definition, it follows that
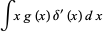 |
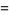 |
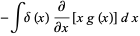 |
(11) |
 |
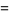 |
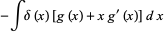 |
(12) |
 |
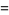 |
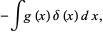 |
(13) |
where the second term can be dropped since 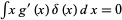 , so (13) implies
, so (13) implies
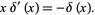 |
(14) |
In general, the same procedure gives
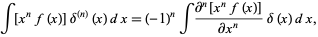 |
(15) |
but since any power of  times
times 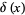 integrates to 0, it follows that only the constant term contributes. Therefore, all terms multiplied by derivatives of
integrates to 0, it follows that only the constant term contributes. Therefore, all terms multiplied by derivatives of 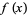 vanish, leaving
vanish, leaving 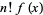 , so
, so
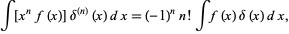 |
(16) |
which implies
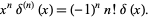 |
(17) |
Other identities involving the derivative of the delta function include
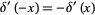 |
(18) |
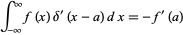 |
(19) |
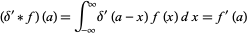 |
(20) |
where 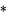 denotes convolution,
denotes convolution,
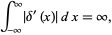 |
(21) |
and
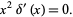 |
(22) |
An integral identity involving 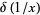 is given by
is given by
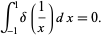 |
(23) |
The delta function also obeys the so-called sifting property
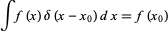 |
(24) |
(Bracewell 1999, pp. 74-75).
A Fourier series expansion of 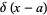 gives
gives
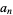 |
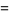 |
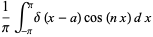 |
(25) |
 |
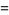 |
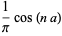 |
(26) |
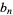 |
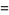 |
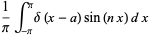 |
(27) |
 |
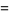 |
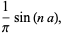 |
(28) |
so
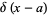 |
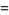 |
![1/(2pi)+1/pisum_(n=1)^(infty)[cos(na)cos(nx)+sin(na)sin(nx)]](http://mathworld.wolfram.com/images/equations/DeltaFunction/Inline58.gif) |
(29) |
 |
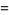 |
![1/(2pi)+1/pisum_(n=1)^(infty)cos[n(x-a)].](http://mathworld.wolfram.com/images/equations/DeltaFunction/Inline61.gif) |
(30) |
The delta function is given as a Fourier transform as
=int_(-infty)^inftye^(-2piikx)dk.](http://mathworld.wolfram.com/images/equations/DeltaFunction/NumberedEquation20.gif) |
(31) |
Similarly,
=int_(-infty)^inftydelta(x)e^(2piikx)dx=1](http://mathworld.wolfram.com/images/equations/DeltaFunction/NumberedEquation21.gif) |
(32) |
(Bracewell 1999, p. 95). More generally, the Fourier transform of the delta function is
=int_(-infty)^inftye^(-2piikx)delta(x-x_0)dx=e^(-2piikx_0).](http://mathworld.wolfram.com/images/equations/DeltaFunction/NumberedEquation22.gif) |
(33) |
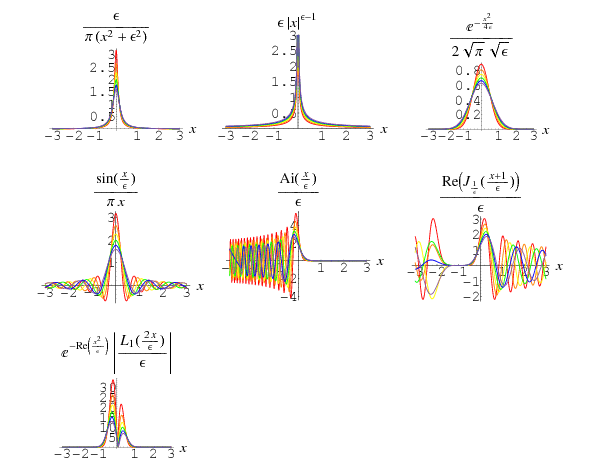
The delta function can be defined as the following limits as 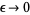 ,
,
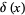 |
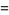 |
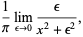 |
(34) |
 |
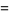 |
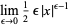 |
(35) |
 |
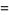 |
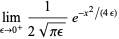 |
(36) |
 |
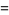 |
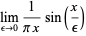 |
(37) |
 |
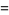 |
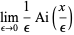 |
(38) |
 |
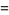 |
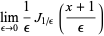 |
(39) |
 |
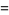 |
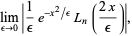 |
(40) |
where 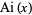 is an Airy function,
is an Airy function, 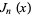 is a Bessel function of the first kind, and
is a Bessel function of the first kind, and 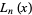 is a Laguerre polynomial of arbitrary positive integer order.
is a Laguerre polynomial of arbitrary positive integer order.

The delta function can also be defined by the limit as 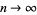
![delta(x)=lim_(n->infty)1/(2pi)(sin[(n+1/2)x])/(sin(1/2x)).](http://mathworld.wolfram.com/images/equations/DeltaFunction/NumberedEquation23.gif) |
(41) |
Delta functions can also be defined in two dimensions, so that in two-dimensional Cartesian coordinates
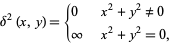 |
(42) |
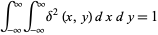 |
(43) |
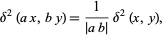 |
(44) |
and
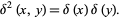 |
(45) |
Similarly, in polar coordinates,
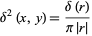 |
(46) |
(Bracewell 1999, p. 85).
In three-dimensional Cartesian coordinates
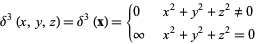 |
(47) |
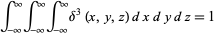 |
(48) |
and
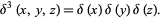 |
(49) |
in cylindrical coordinates 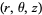 ,
,
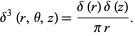 |
(50) |
In spherical coordinates 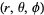 ,
,
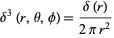 |
(51) |
(Bracewell 1999, p. 85).
A series expansion in cylindrical coordinates gives
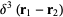 |
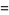 |
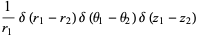 |
(52) |
 |
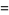 |
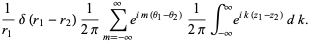 |
(53) |
The solution to some ordinary differential equations can be given in terms of derivatives of 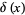 (Kanwal 1998). For example, the differential equation
(Kanwal 1998). For example, the differential equation
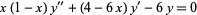 |
(54) |
has classical solution
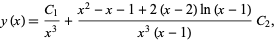 |
(55) |
and distributional solution
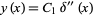 |
(56) |
(M. Trott, pers. comm., Jan. 19, 2006). Note that unlike classical solutions, a distributional solution to an 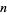 th-order ODE need not contain
th-order ODE need not contain 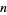 independent constants.
independent constants.
REFERENCES:
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 481-485, 1985.
Bracewell, R. "The Impulse Symbol." Ch. 5 in The Fourier Transform and Its Applications, 3rd ed. New York: McGraw-Hill, pp. 74-104, 2000.
Dirac, P. A. M. Quantum Mechanics, 4th ed. London: Oxford University Press, 1958.
Gasiorowicz, S. Quantum Physics. New York: Wiley, pp. 491-494, 1974.
Kanwal, R. P. "Applications to Ordinary Differential Equations." Ch. 6 in Generalized Functions, Theory and Technique, 2nd ed.Boston, MA: Birkhäuser, pp. 291-255, 1998.
Papoulis, A. Probability, Random Variables, and Stochastic Processes, 2nd ed. New York: McGraw-Hill, pp. 97-98, 1984.
Spanier, J. and Oldham, K. B. "The Dirac Delta Function 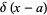 ." Ch. 10 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 79-82, 1987.
." Ch. 10 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 79-82, 1987.
van der Pol, B. and Bremmer, H. Operational Calculus Based on the Two-Sided Laplace Integral. Cambridge, England: Cambridge University Press, 1955.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|