


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 17-9-2018
Date: 15-5-2018
Date: 19-5-2019
|
The lemniscate functions arise in rectifying the arc length of the lemniscate. The lemniscate functions were first studied by Jakob Bernoulli and Giulio Fagnano. A historical account is given by Ayoub (1984), and an extensive discussion by Siegel (1969). The lemniscate functions were the first functions defined by inversion of an integral
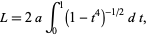 |
(1) |
which was first done by Gauss, who noticed that
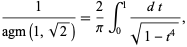 |
(2) |
where 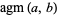 is the arithmetic-geometric mean (Borwein and Bailey 2003, p. 13).
is the arithmetic-geometric mean (Borwein and Bailey 2003, p. 13).
Define the inverse lemniscate functions as
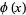 |
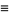 |
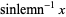 |
(3) |
 |
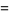 |
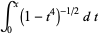 |
(4) |
 |
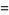 |
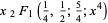 |
(5) |
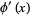 |
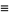 |
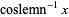 |
(6) |
 |
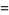 |
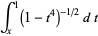 |
(7) |
 |
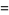 |
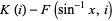 |
(8) |
 |
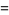 |
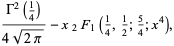 |
(9) |
where 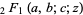 is a hypergeometric function,
is a hypergeometric function, 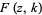 is an incomplete elliptic integral of the first kind,
is an incomplete elliptic integral of the first kind, 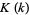 is an elliptic integral of the second kind, and
is an elliptic integral of the second kind, and
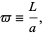 |
(10) |
so that
 |
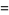 |
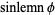 |
(11) |
 |
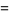 |
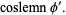 |
(12) |
Now, there is an identity connecting 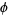 and
and 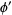 since
since
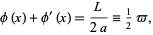 |
(13) |
so
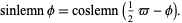 |
(14) |
These functions can be written in terms of Jacobi elliptic functions,
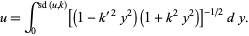 |
(15) |
Now, if 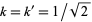 , then
, then
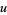 |
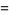 |
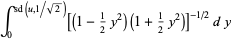 |
(16) |
 |
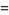 |
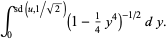 |
(17) |
Let 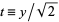 so
so 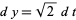 ,
,
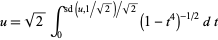 |
(18) |
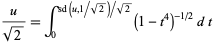 |
(19) |
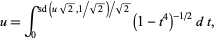 |
(20) |
and
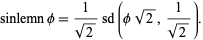 |
(21) |
Similarly,
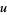 |
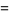 |
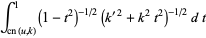 |
(22) |
 |
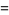 |
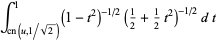 |
(23) |
 |
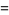 |
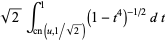 |
(24) |
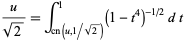 |
(25) |
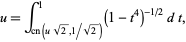 |
(26) |
and
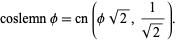 |
(27) |
We know
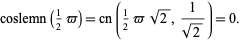 |
(28) |
But it is true that
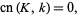 |
(29) |
so
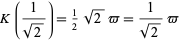 |
(30) |
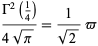 |
(31) |
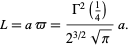 |
(32) |
By expanding 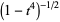 in a binomial series and integrating term by term, the arcsinlemn function can be written
in a binomial series and integrating term by term, the arcsinlemn function can be written
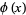 |
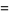 |
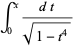 |
(33) |
 |
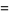 |
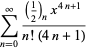 |
(34) |
 |
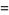 |
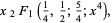 |
(35) |
where 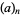 is a Pochhammer symbol (Berndt 1994).
is a Pochhammer symbol (Berndt 1994).
Ramanujan gave the following inversion formula for 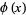 . If
. If
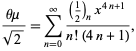 |
(36) |
where
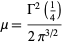 |
(37) |
is the constant obtained by letting 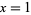 and
and 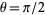 , and
, and
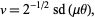 |
(38) |
then
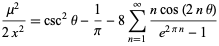 |
(39) |
(Berndt 1994).
Ramanujan also showed that if 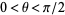 , then
, then
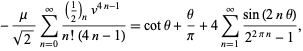 |
(40) |
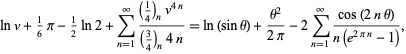 |
(41) |
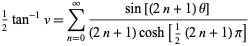 |
(42) |
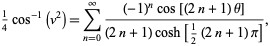 |
(43) |
and
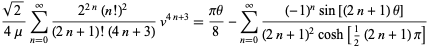 |
(44) |
(Berndt 1994).
A generalized version of the lemniscate function can be defined by letting 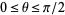 and
and 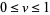 . Write
. Write
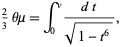 |
(45) |
where 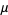 is the constant obtained by setting
is the constant obtained by setting 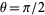 and
and 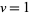 . Then
. Then
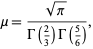 |
(46) |
and Ramanujan showed
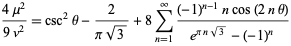 |
(47) |
(Berndt 1994).
REFERENCES:
Ayoub, R. "The Lemniscate and Fagnano's Contributions to Elliptic Integrals." Arch. Hist. Exact Sci. 29, 131-149, 1984.
Berndt, B. C. Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, pp. 245, and 247-255, 258-260, 1994.
Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, 2003.
Siegel, C. L. Topics in Complex Function Theory, Vol. 1. New York: Wiley, 1969.



|
|
|
|
4 أسباب تجعلك تضيف الزنجبيل إلى طعامك.. تعرف عليها
|
|
|
|
|
|
|
أكبر محطة للطاقة الكهرومائية في بريطانيا تستعد للانطلاق
|
|
|
|
|
|
|
العتبة العباسية المقدسة تبحث مع العتبة الحسينية المقدسة التنسيق المشترك لإقامة حفل تخرج طلبة الجامعات
|
|
|