
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 22-5-2019
Date: 10-8-2019
Date: 24-9-2018
|
The Lommel polynomials 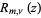 arise from the equation
arise from the equation
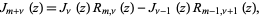 |
(1) |
where 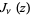 is a Bessel function of the first kind and
is a Bessel function of the first kind and  is a complex number (Watson 1966, p. 294). The function is given for
is a complex number (Watson 1966, p. 294). The function is given for 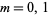 by
by
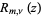 |
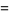 |
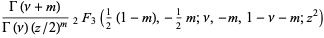 |
(2) |
 |
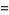 |
![(piz)/(2sin(nupi))[J_(nu+m)(z)J_(-nu+1)(z)+(-1)^mJ_(-nu-m)(z)J_(nu-1)(z)],](http://mathworld.wolfram.com/images/equations/LommelPolynomial/Inline10.gif) |
(3) |
where 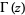 is a gamma function,
is a gamma function, 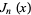 is a Bessel function of the first kind, and
is a Bessel function of the first kind, and 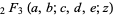 is a generalized hypergeometric function. Since (1) must reduce to the usual recurrence formula for Bessel functions, it follows that
is a generalized hypergeometric function. Since (1) must reduce to the usual recurrence formula for Bessel functions, it follows that
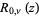 |
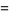 |
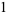 |
(4) |
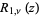 |
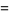 |
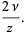 |
(5) |
REFERENCES:
Iyanaga, S. and Kawada, Y. (Eds.). Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, p. 1477, 1980.
Watson, G. N. A Treatise on the Theory of Bessel Functions, 2nd ed. Cambridge, England: Cambridge University Press, p. 294, 1966.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|