المرجع الالكتروني للمعلوماتية
المرجع الألكتروني للمعلوماتية
ENGLISH
آخر المواضيع المضافة

الرياضيات
عدد المواضيع في هذا القسم 9761 موضوعاً
تاريخ الرياضيات
الرياضيات المتقطعة
الجبر
الضبابية
نظرية المجموعات
نظرية الزمر
نظرية الحلقات والحقول
نظرية الاعداد
نظرية الفئات
حساب المتجهات
المتتاليات-المتسلسلات
المصفوفات و نظريتها
المثلثات
الهندسة
التفاضل و التكامل
المعادلات التفاضلية و التكاملية
التحليل
التبلوجيا
نظرية الالعاب
الاحتمالات و الاحصاء
نظرية التحكم
بحوث العمليات
نظرية الكم
الشفرات
الرياضيات التطبيقية
نظريات ومبرهنات
علماء الرياضيات
الرياضيات في العلوم الاخرى
بحوث و اطاريح جامعية
هل تعلم
طرائق التدريس
الرياضيات العامة
نظرية البيان

Untitled Document
أبحث عن شيء أخر المرجع الالكتروني للمعلوماتية
أضيف حديثاً
الضوء
2025-04-10
البلازما والفضاء
2025-04-10
الكون المتحرك
2025-04-10
الفيزياء والكون .. البلازما
2025-04-10
الفيزياء والكون.. الذرة
2025-04-10
D-dimer (Fragment D-dimer, Fibrin degradation product [FDP], Fibrin split products)
2025-04-10

وثائقيات
العباءة العربية .. إرث الآباء واعتزاز الأبناء
التاريخ / 20-09-2024

مختارات
قاعدة « العدول»
21-9-2016
مفهوم الحرارة عند ديموقريطس (القرن 4 ق.م.)
2023-04-16
رقية لوسوسة القلب
18-10-2016
العوامل الجغرافية التي أثرت في حملة كيب الشمالية - التضاريس
18-8-2022
تحليل المسائل الحسابية للصفوف الدنيا-1
15-4-2018
Norlignans
16-5-2019

Fourier-Budan Theorem  
  
1109   02:10 مساءً   date: 4-3-2019
Author : Henrici, P.
Book or Source : Applied and Computational Complex Analysis, Vol. 1: Power Series-Integration-Conformal Mapping-Location of Zeros.New York: Wiley
Page and Part : p. 443


Read More
Schinzel,s Hypothesis
Date: 23-2-2019 817
Rational Polynomial
Date: 17-2-2019 934
Xi-Function
Date: 11-3-2019 2490

Fourier-Budan Theorem

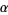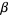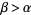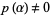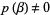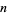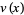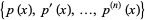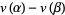For any real alpha and beta such that beta>alpha, let p(alpha)!=0 and p(beta)!=0 be real polynomials of degree n, and v(x) denote the number of sign changes in the sequence . Then the number of zeros in the interval [alpha,beta](each zero counted with proper multiplicity) equals v(alpha)-v(beta) minus an even nonnegative integer.

REFERENCES:

Henrici, P. Applied and Computational Complex Analysis, Vol. 1: Power Series-Integration-Conformal Mapping-Location of Zeros.New York: Wiley, p. 443, 1988.




الجبر أحد الفروع الرئيسية في الرياضيات، حيث إن التمكن من الرياضيات يعتمد على الفهم السليم للجبر. ويستخدم المهندسون والعلماء الجبر يومياً، وتعول المشاريع التجارية والصناعية على الجبر لحل الكثير من المعضلات التي تتعرض لها. ونظراً لأهمية الجبر في الحياة العصرية فإنه يدرّس في المدارس والجامعات في جميع أنحاء العالم. ويُعجب الكثير من الدارسين للجبر بقدرته وفائدته الكبيرتين، إذ باستخدام الجبر يمكن للمرء أن يحل كثيرًا من المسائل التي يتعذر حلها باستخدام الحساب فقط.وجاء اسمه من كتاب عالم الرياضيات والفلك والرحالة محمد بن موسى الخورازمي.


يعتبر علم المثلثات Trigonometry علماً عربياً ، فرياضيو العرب فضلوا علم المثلثات عن علم الفلك كأنهما علمين متداخلين ، ونظموه تنظيماً فيه لكثير من الدقة ، وقد كان اليونان يستعملون وتر CORDE ضعف القوسي قياس الزوايا ، فاستعاض رياضيو العرب عن الوتر بالجيب SINUS فأنت هذه الاستعاضة إلى تسهيل كثير من الاعمال الرياضية.

تعتبر المعادلات التفاضلية خير وسيلة لوصف معظم المـسائل الهندسـية والرياضـية والعلمية على حد سواء، إذ يتضح ذلك جليا في وصف عمليات انتقال الحرارة، جريان الموائـع، الحركة الموجية، الدوائر الإلكترونية فضلاً عن استخدامها في مسائل الهياكل الإنشائية والوصف الرياضي للتفاعلات الكيميائية.
ففي في الرياضيات, يطلق اسم المعادلات التفاضلية على المعادلات التي تحوي مشتقات و تفاضلات لبعض الدوال الرياضية و تظهر فيها بشكل متغيرات المعادلة . و يكون الهدف من حل هذه المعادلات هو إيجاد هذه الدوال الرياضية التي تحقق مشتقات هذه المعادلات.





الأخبار الصحية
لخفض ضغط الدم.. دراسة تحدد "تمارين مهمة"
التاريخ / 2025-04-10

الأخبار العلمية
طال انتظارها.. ميزة جديدة من "واتساب" تعزز الخصوصية
التاريخ / 2025-04-10

الساحة الاسلامية
مشاتل الكفيل تزيّن مجمّع أبي الفضل العبّاس (عليه السلام) بالورد استعدادًا لحفل التخرج المركزي
التاريخ / 2025-04-10