


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 13-2-2019
Date: 13-2-2019
Date: 17-2-2019
|
A polynomial is said to be irreducible if it cannot be factored into nontrivial polynomials over the same field.
For example, in the field of rational polynomials ![Q[x]](http://mathworld.wolfram.com/images/equations/IrreduciblePolynomial/Inline1.gif) (i.e., polynomials
(i.e., polynomials 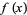 with rational coefficients),
with rational coefficients), 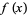 is said to be irreducible if there do not exist two nonconstant polynomials
is said to be irreducible if there do not exist two nonconstant polynomials 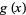 and
and 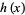 in
in  with rational coefficients such that
with rational coefficients such that
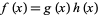 |
(Nagell 1951, p. 160). Similarly, in the finite field GF(2), 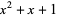 is irreducible, but
is irreducible, but 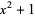 is not, since
is not, since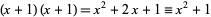 (mod 2).
(mod 2).
Irreducible polynomial checking is implemented in the Wolfram Language as IrreduciblePolynomialQ[poly].
In general, the number of irreducible polynomials of degree 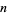 over the finite field GF(
over the finite field GF(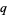 ) is given by
) is given by
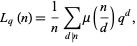 |
where 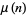 is the Möbius function.
is the Möbius function.
The number of irreducible polynomials of degree 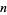 over GF(2) is equal to the number of
over GF(2) is equal to the number of 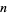 -bead fixed aperiodicnecklaces of two colors and the number of binary Lyndon words of length
-bead fixed aperiodicnecklaces of two colors and the number of binary Lyndon words of length 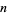 . The first few numbers of irreducible polynomial (mod 2) for
. The first few numbers of irreducible polynomial (mod 2) for 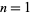 , 2, ... are 2, 1, 2, 3, 6, 9, 18, ... (OEIS A001037). The following table lists the irreducible polynomials (mod 2) of degrees 1 through 5.
, 2, ... are 2, 1, 2, 3, 6, 9, 18, ... (OEIS A001037). The following table lists the irreducible polynomials (mod 2) of degrees 1 through 5.
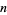 |
irreducible polynomials |
| 1 | 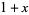 , ,  |
| 2 | 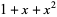 |
| 3 | 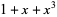 , , 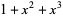 |
| 4 | 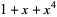 , , 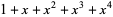 , , 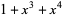 |
| 5 | 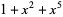 , , 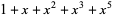 , , 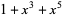 , , 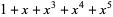 , , 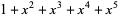 , ,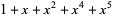 |
The possible polynomial orders of 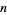 th degree irreducible polynomials over the finite field GF(2) listed in ascending order are given by 1; 3; 7; 5, 15; 31; 9, 21, 63; 127; 17, 51, 85, 255; 73, 511; ... (OEIS A059912).
th degree irreducible polynomials over the finite field GF(2) listed in ascending order are given by 1; 3; 7; 5, 15; 31; 9, 21, 63; 127; 17, 51, 85, 255; 73, 511; ... (OEIS A059912).
REFERENCES:
Marsh, R. Tables of Irreducible Polynomials of GF(2) through Degree 19. Washington, DC: U. S. Dept. Commerce, 1957.
Nagell, T. "Irreducibility of the Cyclotomic Polynomial." §47 in Introduction to Number Theory. New York: Wiley, pp. 160-164, 1951.
Ruskey, F. "Information on Primitive and Irreducible Polynomials." http://www.theory.csc.uvic.ca/~cos/inf/neck/PolyInfo.html.
Sloane, N. J. A. Sequences A001037/M0116 and A059912 in "The On-Line Encyclopedia of Integer Sequences."
Sloane, N. J. A. and Plouffe, S. Figure M0564 in The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|