


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 22-5-2018
Date: 12-7-2018
Date: 23-12-2018
|
A universal differential equation (UDE) is a nontrivial differential-algebraic equation with the property that its solutions approximate to arbitrary accuracy any continuous function on any interval of the real line.
Rubel (1981) found the first known UDE by showing that, given any continuous function 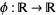 and any positive continuous function
and any positive continuous function 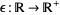 , there exists a
, there exists a 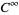 solution
solution 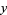 of
of
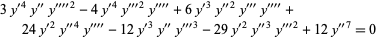 |
(1) |
such that
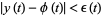 |
(2) |
for all 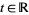 .
.
Duffin (1981) found two additional families of UDEs,
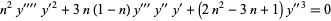 |
(3) |
and
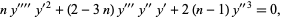 |
(4) |
whose solutions are 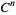 for
for 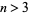 .
.
Briggs (2002) found a further family of UDEs given by
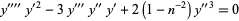 |
(5) |
for 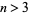 .
.
REFERENCES:
Boshernitzan, M. "Universal Formulae and Universal Differential Equations." Ann. Math. 124, 273-291, 1986.
Boshernitzan, M. and Rubel, L. A. "Coherent Families of Polynomials." Analysis 6, 339-389, 1985.
Briggs, K. "Another Universal Differential Equation." 8 Nov 2002. http://arxiv.org/abs/math.CA/0211142.
Duffin, R. J. "Rubel's Universal Differential Equation." Proc. Nat. Acad. Sci. USA 78, 4661-4662, 1981.
Elsner, C. "On the Approximation of Continuous Functions by 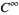 -Solutions of Third-Order Differential Equations." Math. Nachr.157, 235-241, 1992.
-Solutions of Third-Order Differential Equations." Math. Nachr.157, 235-241, 1992.
Elsner, C. "A Universal Functional Equation." Proc. Amer. Math. Soc. 127, 139-143, 1999.
Rubel, L. A. "A Universal Differential Equation." Bull. Amer. Math. Soc. 4, 345-349, 1981.
Rubel, L. A. "Some Research Problems About Algebraic Differential Equations." Trans. Amer. Math. Soc. 280, 43-52, 1983.
Rubel, L. A. "Some Research Problems About Algebraic Differential Equations II." Illinois J. Math. 36, 659-680, 1992.
Rubel, L. A. "Uniform Approximation by Rational Functions All of Which Satisfy the Same Algebraic Differential Equation." J. Approx. Th. 84, 123-128, 1996.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|