


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 22-11-2018
Date: 24-10-2018
Date: 1-11-2018
|
The so-called generalized Fourier integral is a pair of integrals--a "lower Fourier integral" and an "upper Fourier integral"--which allow certain complex-valued functions 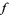 to be decomposed as the sum of integral-defined functions, each of which resembles the usual Fourier integral associated to
to be decomposed as the sum of integral-defined functions, each of which resembles the usual Fourier integral associated to 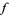 and maintains several key properties thereof.
and maintains several key properties thereof.
Let  be a real variable, let
be a real variable, let 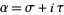 be a complex variable, and let
be a complex variable, and let 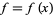 be a function for which
be a function for which 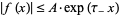 as
as 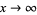 , for which
, for which 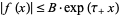 as
as 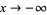 , and for which
, and for which 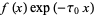 has an analytic Fourier integral where here,
has an analytic Fourier integral where here, 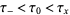 are finite real constants. Next, define the upper and lower generalized Fourier integrals
are finite real constants. Next, define the upper and lower generalized Fourier integrals 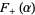 and
and 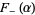 associated to
associated to 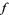 , respectively, by
, respectively, by
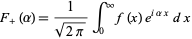 |
(1) |
and
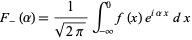 |
(2) |
on the complex regions 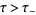 and
and 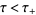 , respectively. Then, for
, respectively. Then, for 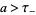 and
and 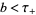 ,
,
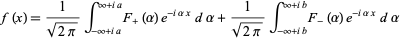 |
(3) |
where the first integral summand equals 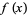 for
for 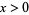 and is zero for
and is zero for 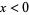 while the second integral summand is zero for
while the second integral summand is zero for 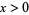 and equals
and equals 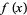 for
for 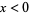 . The decomposition () is called the generalized Fourier integral corresponding to
. The decomposition () is called the generalized Fourier integral corresponding to 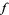 .
.
Note that some literature defines the upper and lower integrals 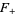 and
and 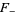 with multiplicative constants different from
with multiplicative constants different from 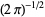 , whereby the identity in () may look slightly different.
, whereby the identity in () may look slightly different.
REFERENCES:
Linton, C. M. and McIver, P. Handbook of Mathematical Techniques for Wave/Structure Interactions. Boca Raton, FL: CRC Press, 2001.
Noble, B. Methods Based on the Wiener-Hopf Technique For the Solution of Partial Differential Equations. Belfast, Northern Ireland: Pergamon Press, 1958.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|