Line Integral

The line integral of a vector field 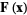 on a curve  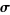is defined by

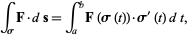(1)

where 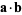 denotes a dot product. In Cartesian coordinates, the line integral can be written

(2)

where

(3)

For 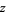 complex and  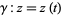a path in the complex plane parameterized by ,

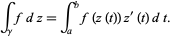(4)

Poincaré's theorem states that if 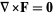 in a simply connected neighborhood  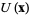of a point , then in this neighborhood, 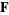 is the gradient of a scalar field ,

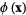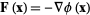(5)

for 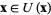, where  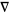is the gradient operator. Consequently, the gradient theorem gives

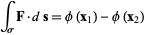(6)

for any path 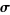 located completely within 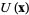, starting at  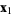and ending at .

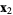This means that if 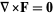 (i.e.,  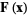is an irrotational field in some region), then the line integral is path-independent in this region. If desired, a Cartesian path can therefore be chosen between starting and ending point to give

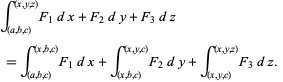(7)

If 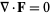 (i.e.,  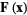is a divergenceless field, a.k.a. solenoidal field), then there exists a vector field  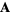such that

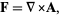(8)

where 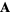 is uniquely determined up to a gradient field (and which can be chosen so that ).

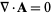REFERENCES:

Krantz, S. G. "The Complex Line Integral." §2.1.6 in Handbook of Complex Variables. Boston, MA: Birkhäuser, p. 22, 1999.