


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 13-7-2018
Date: 25-7-2018
Date: 23-7-2018
|
The partial differential equation
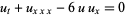 |
(1) |
(Lamb 1980; Zwillinger 1997, p. 175), often abbreviated "KdV." This is a nondimensionalized version of the equation
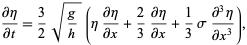 |
(2) |
derived by Korteweg and de Vries (1895) which described weakly nonlinear shallow water waves. Here, 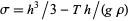 ,
, 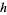 is the channel height,
is the channel height, 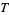 is the surface tension,
is the surface tension, 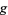 is the gravitational acceleration, and
is the gravitational acceleration, and 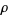 is the density. This equation was found to have solitary wave solutions, vindicating the observations made 51 years earlier of a solitary channel wave by Russell in Aug. 1834 (Russell 1844).
is the density. This equation was found to have solitary wave solutions, vindicating the observations made 51 years earlier of a solitary channel wave by Russell in Aug. 1834 (Russell 1844).
It is a little-known fact that the first genus-2 solution to the Korteweg-de Vries equation was given by Baker (1907; Previato 2004).
Zabusky and Kruskal (1965) subsequently studied the continuum limit of the Fermi-Pasta-Ulam Experiment and, surprisingly, obtained the Korteweg-de Vries equation. They found that the solitary wave solutions had behavior similar to the superposition principle, despite the fact that the waves themselves were highly nonlinear. They dubbed such waves solitons, and proceeded to devise new solution technique for them (Miura et al. 1968). Miura et al. (1968) found nine conservation laws and Miura (1968) found a tenth, hinting that an infinite number of conserved quantities might exist (Tabor 1989, p. 288). In fact, a transformation due to Gardner provides an algorithm for computing an infinite number of conserved densities of the KdV equation, which are connected to those of the so-called modified KdV equation through the Miura transformation
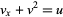 |
(3) |
(Tabor 1989, p. 291). The Korteweg-de Vries equation also exhibits Galilean invariance.
An important step in the solution of the KdV equation was provided by Gardner et al. (1967), who proposed that it could be studied through the properties of the one-dimensional Schrödinger equation for potential 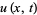
![psi_(xx)-[u(x,y)-lambda]psi=0,](http://mathworld.wolfram.com/images/equations/Korteweg-deVriesEquation/NumberedEquation4.gif) |
(4) |
obtained by making a variable substitution in (3) and using Galilean invariance. If the corresponding quantum mechanical inverse scattering problem (i.e., going from the associated quantum mechanical properties--termed scattering data--to the potential) can be solved, the evolution of 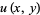 could then be reconstructed without having to actually solve the KdV equation (Tabor 1989, pp. 291-292). While this procedure sounds complicated, and in fact can only be solved exactly for rather special cases, it can be viewed as a more complicated analog of inverse Fourier transforms (which turns out is known as an inverse scattering transform). Using inverse scattering transforms,
could then be reconstructed without having to actually solve the KdV equation (Tabor 1989, pp. 291-292). While this procedure sounds complicated, and in fact can only be solved exactly for rather special cases, it can be viewed as a more complicated analog of inverse Fourier transforms (which turns out is known as an inverse scattering transform). Using inverse scattering transforms, 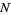 -soliton solutions can be obtained.
-soliton solutions can be obtained.
Lax (1968) showed that the KdV equation is equivalent to the so-called "isospectral integrability condition" for pairs of linear operators, known as Lax pairs (Tabor 1989, p. 304).
The so-called generalized KdV equation is given by
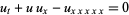 |
(5) |
(Boyd 1986; Zwillinger 1997, p. 175). The so-called deformed KdV equation is given by
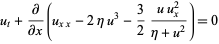 |
(6) |
(Dodd and Fordy 1983; Zwillinger 1997, p. 178), and the modified KdV equation is given by
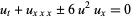 |
(7) |
(Calogero and Degasperis 1982, p. 51; Tabor 1989, p. 304; Zwillinger 1997, p. 178), or
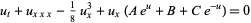 |
(8) |
(Dodd and Fordy 1983; Zwillinger 1997, p. 178).
The cylindrical KdV equation is given by
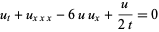 |
(9) |
(Calogero and Degasperis 1982, p. 50; Zwillinger 1997, p. 175), and the spherical KdV by
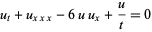 |
(10) |
(Calogero and Degasperis 1982, p. 51; Zwillinger 1997, p. 175).
REFERENCES:
Baker, H. F. An Introduction to the Theory of Multiply Periodic Functions. London: Cambridge University Press, 1907.
Baker, H. F. Abelian Functions: Abel's Theorem and the Allied Theory, Including the Theory of the Theta Functions. New York: Cambridge University Press, p. xix, 1995.
Boyd, J. P. "Solitons from Sine Waves: Analytical and Numerical Methods of Non-Integrable Solitary and Cnoidal Waves." Physica D 21, 227-246, 1986.
Calogero, F. and Degasperis, A. Spectral Transform and Solitons: Tools to Solve and Investigate Nonlinear Evolution Equations.New York: North-Holland, 1982.
Dodd, R. and Fordy, A. "The Prolongation Structures of Quasi-Polynomial Flows." Proc. Roy. Soc. A 385, 389-429, 1983.
Gardner, C. S. "The Korteweg-de Vries Equation and Generalizations, IV. The Korteweg-de Vries Equation as a Hamiltonian System." J. Math. Phys. 12, 1548-1551, 1971.
Gardner, C. S.; Greene, C. S.; Kruskal, M. D.; and Miura, R. M. "Method for Solving the Korteweg-de Vries Equation." Phys. Rev. Lett. 19, 1095-1097, 1967.
Infeld, E. and Rowlands, G. Nonlinear Waves, Solitons, and Chaos, 2nd ed. Cambridge, England: Cambridge University Press, 2000.
Korteweg, D. J. and de Vries, F. "On the Change of Form of Long Waves Advancing in a Rectangular Canal, and on a New Type of Long Stationary Waves." Philos. Mag. 39, 422-443, 1895.
Lamb, G. L. Jr. Ch. 4 in Elements of Soliton Theory. New York: Wiley, 1980.
Lax, P. "Integrals of Nonlinear Evolution Equations and Solitary Waves." Comm. Pure Appl. Math. 21, 467-490, 1968.
Miles, J. W. "The Korteweg-de Vries Equation, A Historical Essay." J. Fluid Mech. 106, 131-147, 1981.
Miura, R. M. "Korteweg-de Vries Equation and Generalizations. I. A Remarkable Explicit Nonlinear Transformation." J. Math. Phys. 9, 1202-1204, 1968.
Miura, R. M.; Gardner, C. S.; and Kruskal, M. D. "Korteweg-de Vries Equation and Generalizations. II. Existence of Conservation Laws and Constants of Motion." J. Math. Phys. 9, 1204-1209, 1968.
Previato, E. "Featured Review: CRC Concise Encyclopedia of Mathematics. Second Edition." SIAM Rev. 46, 349-354, 2004.
Russell, J. S. "Report on Waves." Report of the 14th Meeting of the British Association for the Advancement of Science. London: John Murray, pp. 311-390, 1844.
Segal, G. "The Geometry of the KdV Equation." Int. J. Mod. Phys. 6, 2859-2869, 1991.
Tabor, M. "Nonlinear Evolution Equations and Solitons." Ch. 7 in Chaos and Integrability in Nonlinear Dynamics: An Introduction.New York: Wiley, pp. 278-321, 1989.
Zabusky, N. J. and Kruskal, M. D. "Interaction of Solitons in a Collisionless Plasma and the Recurrence of Initial States." Phys. Rev. Let. 15, 240-243, 1965.
Zakharov, V. E. and Faddeev, L. D. "Korteweg-de Vries Equation, A Completely Integrable System." Funct. Anal. Appl. 5, 280-287, 1971.
Zwillinger, D. (Ed.). CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, p. 417, 1995.
Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, p. 131, 1997.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|