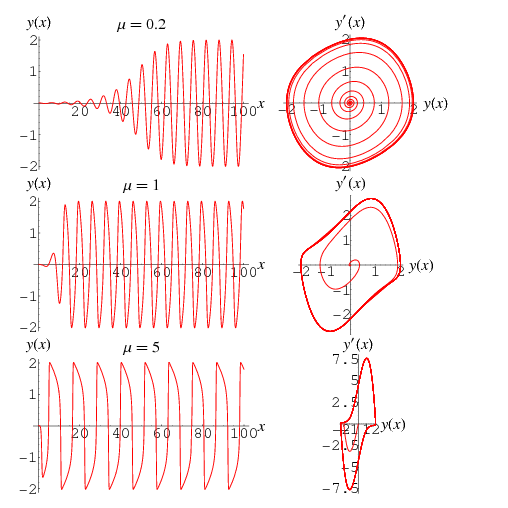
The van der Pol equation is an ordinary differential equation that can be derived from the Rayleigh differential equationby differentiating and setting 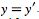 . It is an equation describing self-sustaining oscillations in which energy is fed into small oscillations and removed from large oscillations. This equation arises in the study of circuits containing vacuum tubes and is given by

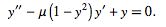
If 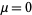, the equation reduces to the equation of simple harmonic motion

REFERENCES:

Birkhoff, G. and Rota, G.-C. Ordinary Differential Equations, 3rd ed. New York: Wiley, p. 134, 1978.

Boyce, W. E. and DiPrima, R. C. Elementary Differential Equations and Boundary Value Problems, 4th ed. New York: Wiley, 1986.

Kreyszig, E. Advanced Engineering Mathematics, 6th ed. New York: Wiley, pp. 496-500, 1988.

Wiggins, S. Introduction to Applied Nonlinear Dynamical Systems and Chaos. New York: Springer-Verlag, p. 179, 1990.

Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, p. 127, 1997.

اخر الاخبار

اخبار العتبة العباسية المقدسة

العتبة العباسية المقدسة تواصل تنظيم مجالس العزاء الصباحية بذكرى زيارة عاشوراء

مواكب العزاء تستذكر في التاسع من شهر المحرم شهادة عبدالله الرضيع بن الحسين (عليهما السلام)

العتبة العباسية المقدسة تستذكر تضحيات القاسم بن الحسن (عليهما السلام)

شعبة الحرم الشريف تواصل تنفيذ خطتها الخاصة بشهر المحرّم داخل مرقد أبي الفضل العباس (عليه السلام)

المزيد

الآخبار الصحية

لهذا السبب.. إغلاق 25 مركزًا لعلاج الإدمان في مصر ؟

خلافا للاعتقاد الشائع.. علماء يكشفون أسرار بذور البطيخ ؟!

هذا ما يحدث لجسمك عند تناولك الطماطم بانتظام !

تعرف على أطعمة تسرّع "تعافي الجسم" من حروق الشمس

المزيد

الآخبار التكنلوجية

الثلوج تغطي الصحراء الأكثر جفافا في العالم!

بتلسكوب "ألما".. التقاط صورا غير مسبوقة لبدايات الكون !

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

المزيد