


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 13-6-2018
Date: 5-7-2018
Date: 13-6-2018
|
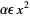 ,
,
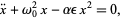 |
(1) |
find the first-order solution using a perturbation method. Write
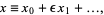 |
(2) |
and plug back into (1) and group powers to obtain
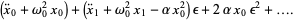 |
(3) |
To solve this equation, keep terms only to order 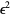 and note that, because this equation must hold for all powers of
and note that, because this equation must hold for all powers of 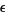 , we can separate it into the two simultaneous differential equations
, we can separate it into the two simultaneous differential equations
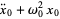 |
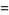 |
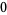 |
(4) |
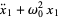 |
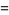 |
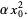 |
(5) |
Setting our clock so that 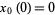 , the solution to (4) is then
, the solution to (4) is then
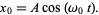 |
(6) |
Plugging this solution back into (5) then gives
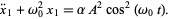 |
(7) |
The equation can be solved to give
![x_1=(alphaA^2)/(6omega_0^2)[3-cos(2omega_0t)]+C_1cos(omega_0t)+C_2sin(omega_0t),](http://mathworld.wolfram.com/images/equations/SimpleHarmonicMotionQuadraticPerturbation/NumberedEquation6.gif) |
(8) |
Combining 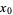 and
and 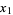 then gives
then gives
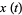 |
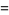 |
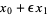 |
(9) |
 |
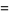 |
![Acos(omega_0t)-(alphaA^2)/(6omega_0^2)epsilon[cos(2omega_0t)-3],](http://mathworld.wolfram.com/images/equations/SimpleHarmonicMotionQuadraticPerturbation/Inline18.gif) |
(10) |
where the sinusoidal and cosinusoidal terms of order 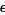 (from the
(from the 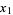 ) have been ignored in comparison with the larger terms from
) have been ignored in comparison with the larger terms from 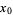 .
.
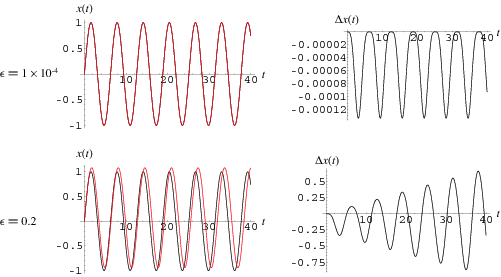
As can be seen in the top figure above, this solution approximates 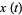 only for
only for 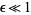 . As the lower figure shows, the differences from the unperturbed oscillator grow stronger over time for even relatively small values of
. As the lower figure shows, the differences from the unperturbed oscillator grow stronger over time for even relatively small values of 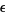 .
.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|