Separation of Variables

Separation of variables is a method of solving ordinary and partial differential equations.

For an ordinary differential equation

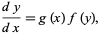(1)

where 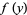is nonzero in a neighborhood of the initial value, the solution is given implicitly by

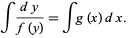(2)

If the integrals can be done in closed form and the resulting equation can be solved for 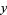 (which are two pretty big "if"s), then a complete solution to the problem has been obtained. The most important equation for which this technique applies is  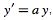, the equation for exponential growth and decay (Stewart 2001).

For a partial differential equation in a function 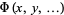 and variables , , 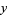..., separation of variables can be applied by making a substitution of the form

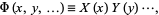(3)

breaking the resulting equation into a set of independent ordinary differential equations, solving these for 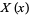, , 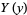..., and then plugging them back into the original equation.

This technique works because if the product of functions of independent variables is a constant, each function must separately be a constant. Success requires choice of an appropriate coordinate system and may not be attainable at all depending on the equation. Separation of variables was first used by L'Hospital in 1750. It is especially useful in solving equations arising in mathematical physics, such as Laplace's equation, the Helmholtz differential equation, and the Schrödinger equation.

REFERENCES:

Arfken, G. "Separation of Variables" and "Separation of Variables--Ordinary Differential Equations." §2.6 and §8.3 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 111-117 and 448-451, 1985.

Bateman, H. Partial Differential Equations of Mathematical Physics. New York: Dover, 1944.

Brown, J. W. and Churchill, R. V. Fourier Series and Boundary Value Problems, 5th ed. New York: McGraw-Hill, 1993.

Byerly, W. E. An Elementary Treatise on Fourier's Series, and Spherical, Cylindrical, and Ellipsoidal Harmonics, with Applications to Problems in Mathematical Physics. New York: Dover, 1959.

Courant, R. and Hilbert, D. Methods of Mathematical Physics, Vol. 1. New York: Wiley, 1989.

Courant, R. and Hilbert, D. Methods of Mathematical Physics, Vol. 2. New York: Wiley, 1989.

Eisenhart, L. P. "Separable Systems in Euclidean 3-Space." Physical Review 45, 427-428, 1934.

Eisenhart, L. P. "Separable Systems of Stäckel." Ann. Math. 35, 284-305, 1934.

Eisenhart, L. P. "Potentials for Which Schroedinger Equations Are Separable." Phys. Rev. 74, 87-89, 1948.

Frank, P. and Mises, R. von. Die Differential- und Integralgleichungen der Mechanik und Physik, 8th ed., erster mathematischer Teil. Braunschweig, Germany: Vieweg, 1930.

Frank, P. and Mises, R. von. Die Differential- und Integralgleichungen der Mechanik und Physik, 8th ed., zweiter physikalischer Teil. Braunschweig, Germany: Vieweg, 1930.

Hildebrand, F. B. Advanced Calculus for Engineers. Englewood Cliffs, NJ: Prentice-Hall, 1949.

Jeffreys, S. H. and Jeffreys, B. S. Methods of Mathematical Physics, 3rd ed. Cambridge, England: Cambridge University Press, 1988.

Kellogg, O. D. Foundations of Potential Theory. New York: Dover, 1953.

Lense, J. Reihenentwicklungen in der mathematischen Physik. Berlin: de Gruyter, 1933.

Maxwell, J. C. A Treatise on Electricity and Magnetism, Vol. 1, unabridged 3rd ed. New York: Dover, 1954.

Maxwell, J. C. A Treatise on Electricity and Magnetism, Vol. 2, unabridged 3rd ed. New York: Dover, 1954.

Miller, W. Jr. Symmetry and Separation of Variables. Reading, MA: Addison-Wesley, 1977.

Moon, P. and Spencer, D. E. "Separability Conditions for the Laplace and Helmholtz Equations." J. Franklin Inst. 253, 585-600, 1952.

Moon, P. and Spencer, D. E. "Theorems on Separability in Riemannian n-space." Proc. Amer. Math. Soc. 3, 635-642, 1952.

Moon, P. and Spencer, D. E. "Recent Investigations of the Separation of Laplace's Equation." Proc. Amer. Math. Soc. 4, 302-307, 1953.

Moon, P. and Spencer, D. E. "Separability in a Class of Coordinate Systems." J. Franklin Inst. 254, 227-242, 1952.

Moon, P. and Spencer, D. E. Field Theory for Engineers. Princeton, NJ: Van Nostrand, 1961.

Moon, P. and Spencer, D. E. "Eleven Coordinate Systems." §1 in Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions, 2nd ed. New York: Springer-Verlag, pp. 1-48, 1988.

Morse, P. M. and Feshbach, H. "Separable Coordinates" and "Table of Separable Coordinates in Three Dimensions." §5.1 in Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 464-523 and 655-666, 1953.

Murnaghan, F. D. Introduction to Applied Mathematics. New York: Wiley, 1948.

Smythe, W. R. Static and Dynamic Electricity, 3rd ed., rev. pr. New York: Hemisphere, 1989.

Sommerfeld, A. Partial Differential Equations in Physics. New York: Academic Press, 1964.

Stewart, J. Calculus: Concepts and Contexts, 2nd ed. Brooks/Cole, 2001.

Weber, E. Electromagnetic Fields: Theory and Applications. New York: Wiley, 1950.

Webster, A. G. Partial Differential Equations of Mathematical Physics, 2nd corr. ed. New York: Dover, 1955.