
Indicial Equation
 المؤلف:
Morse, P. M. and Feshbach, H
المؤلف:
Morse, P. M. and Feshbach, H
 المصدر:
Methods of Theoretical Physics, Part I. New York: McGraw-Hill
المصدر:
Methods of Theoretical Physics, Part I. New York: McGraw-Hill
 الجزء والصفحة:
pp. 532-534
الجزء والصفحة:
pp. 532-534
 13-6-2018
13-6-2018
 1351
1351
Indicial Equation
An indicial equation, also called a characteristic equation, is a recurrence equation obtained during application of the Frobenius method of solving a second-order ordinary differential equation. The indicial equation is obtained by noting that, by definition, the lowest order term 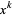 (that corresponding to
(that corresponding to 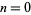 ) must have a coefficient of zero.
) must have a coefficient of zero.
1. If the two roots are equal, only one solution can be obtained.
2. If the two roots differ by a noninteger, two solutions can be obtained.
3. If the two roots differ by an integer, the larger will yield a solution. The smaller may or may not.
For an example of the construction of an indicial equation, see Bessel function of the first kind.
The following table gives the indicial equations for some common differential equations.
| differential equation |
indicial equation |
| Bessel differential equation |
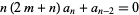 |
| Chebyshev differential equation |
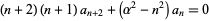 |
| Hermite differential equation |
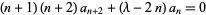 |
| Jacobi differential equation |
![[n(n+alpha+beta+1)-nu(nu+alpha+beta+1)]a_nu-2(nu+1)(nu+alpha+1)a_(nu+1)=0](http://mathworld.wolfram.com/images/equations/IndicialEquation/Inline6.gif) |
| Laguerre differential equation |
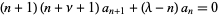 |
| Legendre differential equation |
![(n+1)(n+2)a_(n+2)+[-n(n+1)+l(l+1)]a_n=0](http://mathworld.wolfram.com/images/equations/IndicialEquation/Inline8.gif) |
REFERENCES:
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 532-534, 1953.
 الاكثر قراءة في معادلات تفاضلية
الاكثر قراءة في معادلات تفاضلية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


