The measurement of entropy
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
91
2025-11-05
26
The measurement of entropy
The entropy of a system at a temperature T is related to its entropy at T = 0 by measuring its heat capacity Cp at different temperatures and evaluating the integral in eqn 3.18, taking care to add the entropy of transition (∆trsH/Ttrs) for each phase transition between T =0 and the temperature of interest. For example, if a substance melts at Tf and boils at Tb, then its entropy above its boiling temperature is given by
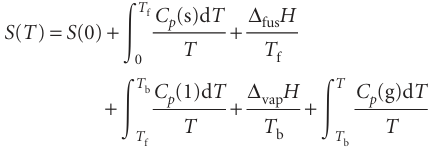
All the properties required, except S(0), can be measured calorimetrically, and the integrals can be evaluated either graphically or, as is now more usual, by fitting a polynomial to the data and integrating the polynomial analytically. The former procedure is illustrated in Fig. 3.14: the area under the curve of Cp/T against T is the integral required. Because dT/T = d ln T, an alternative procedure is to evaluate the area under a plot of Cp against ln T.
One problem with the determination of entropy is the difficulty of measuring heat capacities near T = 0. There are good theoretical grounds for assuming that the heat capacity is proportional to T3 when T is low (see Section 8.1), and this dependence is the basis of the Debye extrapolation. In this method, Cp is measured down to as low a temperature as possible, and a curve of the form aT3 is fitted to the data. That fit determines the value of a, and the expression Cp = aT3 is assumed valid down to T = 0.
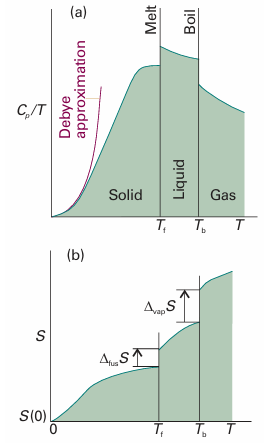
Fig. 3.14 The calculation of entropy from heat capacity data. (a) The variation of Cp/T with the temperature for a sample. (b) The entropy, which is equal to the area beneath the upper curve up to the corresponding temperature, plus the entropy of each phase transition passed.
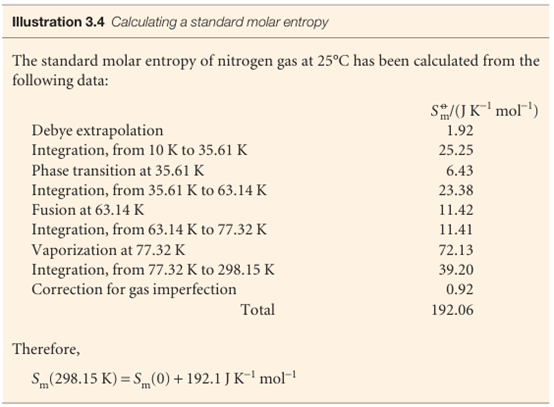
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
