
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Shock waves
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المصدر:
The Feynman Lectures on Physics
الجزء والصفحة:
Volume I, Chapter 51
2024-06-30
1581
Wave speed often depends on the amplitude, and in the case of sound the speed depends upon the amplitude in the following way. An object moving through the air has to move the air out of the way, so the disturbance produced in this case is some kind of a pressure step, with the pressure higher behind the wavefront than in the undisturbed region not yet reached by the wave (running along at the normal speed, say). But the air that is left behind, after the wavefront passes, has been compressed adiabatically, and therefore the temperature is increased. Now the speed of sound increases with the temperature, so the speed in the region behind the jump is faster than in the air in front. That means that any other disturbance that is made behind this step, say by a continuous pushing of the body, or any other disturbance, will ride faster than the front, the speed increasing with higher pressure. Figure 51–3 illustrates the situation, with some little bumps of pressure added to the pressure contour to aid visualization. We see that the higher-pressure regions at the rear overtake the front as time goes on, until ultimately the compressional wave develops a sharp front. If the strength is very high, “ultimately” means right away; if it is rather weak, it takes a long time; it may be, in fact, that the sound is spreading and dying out before it has time to do this.
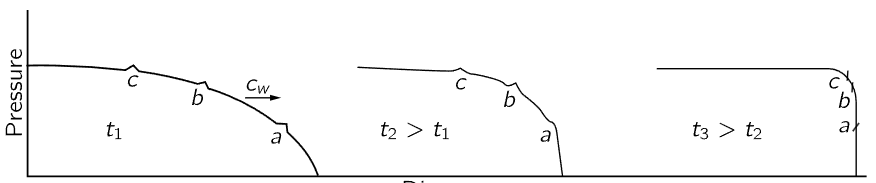
Fig. 51–3. Wavefront “snapshots” at successive instants in time.
The sounds we make in talking are extremely weak relative to the atmospheric pressure—only 1 part in a million or so. But for pressure changes of the order of 1 atmosphere, the wave velocity increases by about twenty percent, and the wavefront sharpens up at a correspondingly high rate. In nature nothing happens infinitely rapidly, presumably, and what we call a “sharp” front has, actually, a very slight thickness; it is not infinitely steep. The distances over which it is varying are of the order of one mean free path, in which the theory of the wave equation begins to fail because we did not consider the structure of the gas.
Now, referring again to Fig. 51–2, we see that the curvature can be understood if we appreciate that the pressures near the apex are higher than they are farther back, and so the angle θ is greater. That is, the curve is the result of the fact that the speed depends upon the strength of the wave. Therefore, the wave from an atomic bomb explosion travels much faster than the speed of sound for a while, until it gets so far out that it is weakened to such an extent from spreading that the pressure bump is small compared with atmospheric pressure. The speed of the bump then approaches the speed of sound in the gas into which it is going. (Incidentally, it always turns out that the speed of the shock is higher than the speed of sound in the gas ahead, but is lower than the speed of sound in the gas behind. That is, impulses from the back will arrive at the front, but the front rides into the medium in which it is going faster than the normal speed of signals. So, one cannot tell, acoustically, that the shock is coming until it is too late. The light from the bomb arrives first, but one cannot tell that the shock is coming until it arrives, because there is no sound signal coming ahead of it.)

Figure 51–4
This is a very interesting phenomenon, this piling up of waves, and the main point on which it depends is that after a wave is present, the speed of the resulting wave should be higher. Another example of the same phenomenon is the following. Consider water flowing in a long channel with finite width and finite depth. If a piston, or a wall across the channel, is moved along the channel fast enough, water piles up, like snow before a snow plow. Now suppose the situation is as shown in Fig. 51–4, with a sudden step in water height somewhere in the channel. It can be demonstrated that long waves in a channel travel faster in deeper water than they do in shallow water. Therefore, any new bumps or irregularities in energy supplied by the piston run off forward and pile up at the front. Again, ultimately what we have is just water with a sharp front, theoretically. However, as Fig. 51–4 shows, there are complications. Pictured is a wave coming up a channel; the piston is at the far-right end of the channel. At first it might have appeared like a well-behaved wave, as one might expect, but farther along the channel, it has become sharper and sharper until the events pictured occurred. There is a terrible churning at the surface, as the pieces of water fall down, but it is essentially a very sharp rise with no disturbance of the water ahead.
Actually water is much more complicated than sound. However, just to illustrate a point, we will try to analyze the speed of such a so-called bore, in a channel. The point here is not that this is of any basic importance for our purposes—it is not a great generalization—it is only to illustrate that the laws of mechanics that we already know are capable of explaining the phenomenon.
Imagine, for a moment, that the water does look something like Fig. 51–5(a), that water at the higher height h2 is moving with a velocity v, and that the front is moving with velocity u into undisturbed water which is at height h1. We would like to determine the speed at which the front moves. In a time Δt a vertical plane initially at x1 moves a distance vΔt to x2, while the front of the wave has moved uΔt.
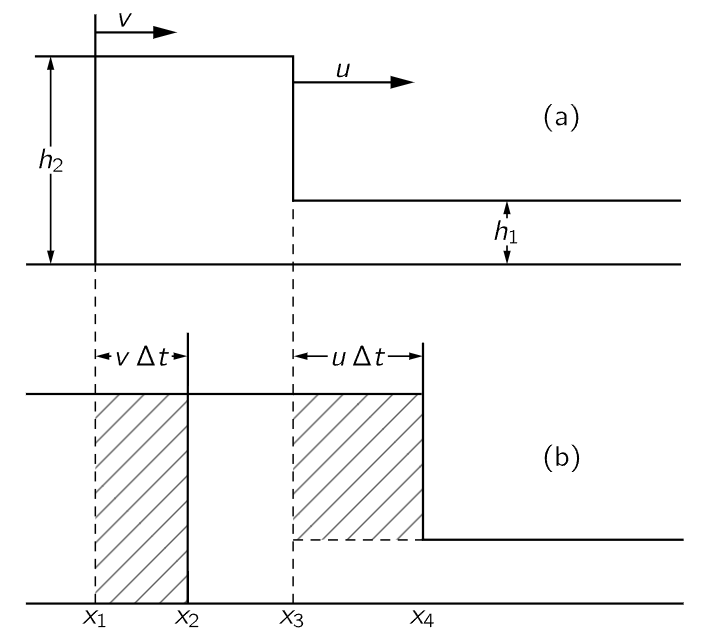
Fig. 51–5. Two cross sections of a bore in a channel, with (b) at an interval Δt later than (a).
Now we apply the equations of conservation of matter and momentum. First, the former: Per unit channel width, we see that the amount h2vΔt of matter that has moved past x1 (shown shaded) is compensated by the other shaded region, which amounts to (h2−h1)uΔt. So, dividing by Δt, vh2=u(h2−h1). That does not yet give us enough, because although we have h2 and h1, we do not know either u or v; we are trying to get both of them.
Now the next step is to use conservation of momentum. We have not discussed the problems of water pressure, or anything in hydrodynamics, but it is clear anyway that the pressure of water at a given depth is just enough to hold up the column of water above it. Therefore, the pressure of water is equal to ρ, the density of water, times g, times the depth below the surface. Since the pressure increases linearly with depth, the average pressure over the plane at x1, say, is (1/2) ρgh2, which is also the average force per unit width and per unit height pushing the plane toward x2. So we multiply by another h2 to get the total force which is acting on the water pushing from the left. On the other hand, there is pressure in the water on the right also, exerting an opposite force on the region in question, which is, by the same kind of analysis, (1/2)ρgh21. Now we must balance the forces against the rate of change of the momentum. Thus, we have to figure out how much more momentum there is in situation (b) in Fig. 51–5 than there was in (a). We see that the additional mass that has acquired the speed v is just ρh2uΔt−ρh2vΔt (per unit width), and multiplying this by v gives the additional momentum to be equated to the impulse FΔt:
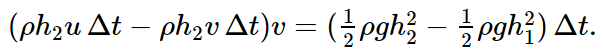
If we eliminate v from this equation by substituting vh2=u(h2−h1), already found, and simplify, we get finally that u2=gh2(h1+h2)/2h1.
If the height difference is very small, so that h1 and h2 are nearly equal, this says that the velocity 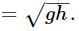 As we will see later, that is only true provided the wavelength of the wave is longer than the depth of the channel.
As we will see later, that is only true provided the wavelength of the wave is longer than the depth of the channel.
We could also do the analogous thing for sound waves—including the conservation of internal energy, not the conservation of entropy, because the shock is irreversible. In fact, if one checks the conservation of energy in the bore problem, one finds that energy is not conserved. If the height difference is small, it is almost perfectly conserved, but as soon as the height difference becomes very appreciable, there is a net loss of energy. This is manifested as the falling water and the churning shown in Fig. 51–4.
In shock waves there is a corresponding apparent loss of energy, from the point of view of adiabatic reactions. The energy in the sound wave, behind the shock, goes into heating of the gas after shock passes, corresponding to churning of the water in the bore. In working it out, three equations for the sound case turn out to be necessary for solution, and the temperature behind the shock is not the same as the temperature in front, as we have seen.
If we try to make a bore that is upside down (h2<h1), then we find that the energy loss per second is negative. Since energy is not available from anywhere, that bore cannot then maintain itself; it is unstable. If we were to start a wave of that sort, it would flatten out, because the speed dependence on height that resulted in sharpening in the case, we discussed would now have the opposite effect.
 الاكثر قراءة في الفيزياء العامة
الاكثر قراءة في الفيزياء العامة
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















