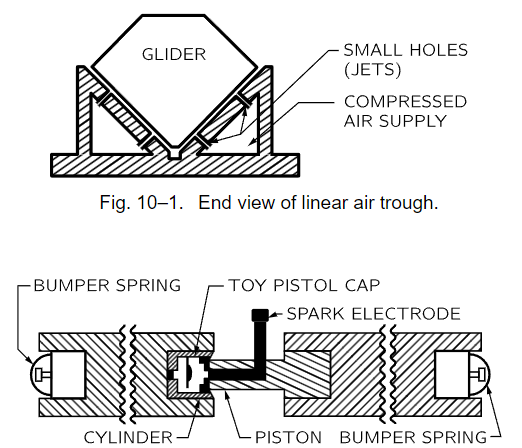
Fig. 10–2. Sectional view of gliders with explosive interaction cylinder attachment.

We can verify the above assumptions experimentally: first, that if two stationary objects of equal mass are separated by an explosion they will move apart with the same speed, and second, if two objects of equal mass, coming together with the same speed, collide and stick together they will stop. This we can do by means of a marvelous invention called an air trough,¹ which gets rid of friction, the thing which continually bothered Galileo (Fig. 10–1). He could not do experiments by sliding things because they do not slide freely, but, by adding a magic touch, we can today get rid of friction. Our objects will slide without difficulty, on and on at a constant velocity, as advertised by Galileo. This is done by supporting the objects on air. Because air has very low friction, an object glides along with practically constant velocity when there is no applied force. First, we use two glide blocks which have been made carefully to have the same weight, or mass (their weight was measured really, but we know that this weight is proportional to the mass), and we place a small explosive cap in a closed cylinder between the two blocks (Fig. 10–2). We shall start the blocks from rest at the center point of the track and force them apart by exploding the cap with an electric spark. What should happen? If the speeds are equal when they fly apart, they should arrive at the ends of the trough at the same time. On reaching the ends they will both bounce back with practically opposite velocity, and will come together and stop at the center where they started. It is a good test; when it is actually done the result is just as we have described (Fig. 10–3).

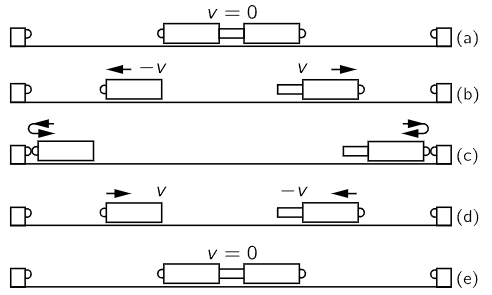
Fig. 10–3. Schematic view of action-reaction experiment with equal masses.

Now the next thing we would like to figure out is what happens in a less simple situation. Suppose we have two equal masses, one moving with velocity v and the other standing still, and they collide and stick; what is going to happen? There is a mass 2m altogether when we are finished, drifting with an unknown velocity. What velocity? That is the problem. To find the answer, we make the assumption that if we ride along in a car, physics will look the same as if we are standing still. We start with the knowledge that two equal masses, moving in opposite directions with equal speeds v, will stop dead when they collide. Now suppose that while this happens, we are riding by in an automobile, at a velocity −v. Then what does it look like? Since we are riding along with one of the two masses which are coming together, that one appears to us to have zero velocity. The other mass, however, going the other way with velocity v, will appear to be coming toward us at a velocity 2v (Fig. 10–4). Finally, the combined masses after collision will seem to be passing by with velocity v. We therefore conclude that an object with velocity 2v, hitting an equal one at rest, will end up with velocity v, or what is mathematically exactly the same, an object with velocity v hitting and sticking to one at rest will produce an object moving with velocity v/2. Note that if we multiply the mass and the velocity beforehand and add them together, mv+0, we get the same answer as when we multiply the mass and the velocity of everything afterwards, 2m times v/2. So that tells us what happens when a mass of velocity v hits one standing still.

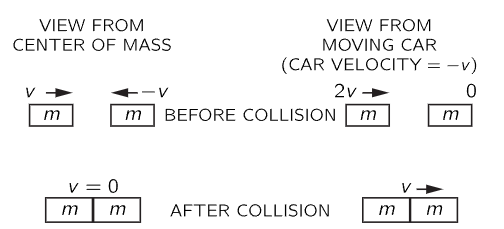
Fig. 10–4. Two views of an inelastic collision between equal masses.

In exactly the same manner we can deduce what happens when equal objects having any two velocities hit each other.

Fig. 10–5. Two views of another inelastic collision between equal masses.

Suppose we have two equal bodies with velocities v₁ and v₂, respectively, which collide and stick together. What is their velocity v after the collision? Again, we ride by in an automobile, say at velocity v₂, so that one body appears to be at rest. The other then appears to have a velocity v₁−v₂, and we have the same case that we had before. When it is all finished, they will be moving at 1/2(v₁−v₂) with respect to the car. What then is the actual speed on the ground? It is (Fig. 10–5). Again we note that

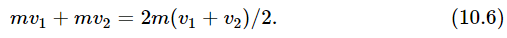
Thus, using this principle, we can analyze any kind of collision in which two bodies of equal mass hit each other and stick. In fact, although we have worked only in one dimension, we can find out a great deal about much more complicated collisions by imagining that we are riding by in a car in some oblique direction. The principle is the same, but the details get somewhat complicated.

In order to test experimentally whether an object moving with velocity v, colliding with an equal one at rest, forms an object moving with velocity v/2, we may perform the following experiment with our air-trough apparatus. We place in the trough three equally massive objects, two of which are initially joined together with our explosive cylinder device, the third being very near to but slightly separated from these and provided with a sticky bumper so that it will stick to another object which hits it. Now, a moment after the explosion, we have two objects of mass m moving with equal and opposite velocities v. A moment after that, one of these collides with the third object and makes an object of mass 2m moving, so we believe, with velocity v/2. How do we test whether it is really v/2? By arranging the initial positions of the masses on the trough so that the distances to the ends are not equal, but are in the ratio 2:1. Thus our first mass, which continues to move with velocity v, should cover twice as much distance in a given time as the two which are stuck together (allowing for the small distance travelled by the second object before it collided with the third). The mass m and the mass 2m should reach the ends at the same time, and when we try it, we find that they do (Fig. 10–6).

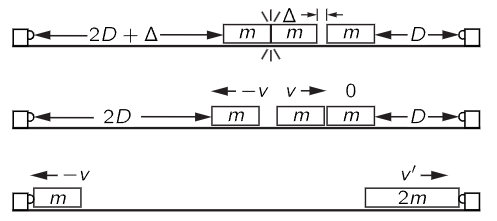
Fig. 10–6. An experiment to verify that a mass m with velocity v striking a mass m with zero velocity gives 2m with velocity v/2.

The next problem that we want to work out is what happens if we have two different masses. Let us take a mass m and a mass 2m and apply our explosive interaction. What will happen then? If, as a result of the explosion, m moves with velocity v, with what velocity does 2m move? The experiment we have just done may be repeated with zero separation between the second and third masses, and when we try it, we get the same result, namely, the reacting masses m and 2m attain velocities −v and v/2. Thus, the direct reaction between m and 2m gives the same result as the symmetrical reaction between m and m, followed by a collision between m and a third mass m in which they stick together. Furthermore, we find that the masses m and 2m returning from the ends of the trough, with their velocities (nearly) exactly reversed, stop dead if they stick together.

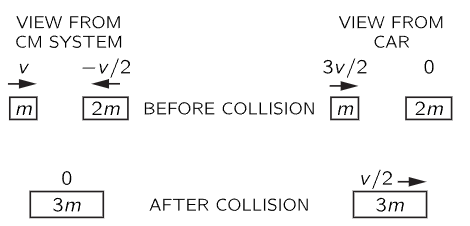
Fig. 10–7. Two views of an inelastic collision between m and 2m.

Now the next question we may ask is this. What will happen if a mass m with velocity v, say, hits and sticks to another mass 2m at rest? This is very easy to answer using our principle of Galilean relativity, for we simply watch the collision which we have just described from a car moving with velocity −v/2 (Fig. 10–7). From the car, the velocities are

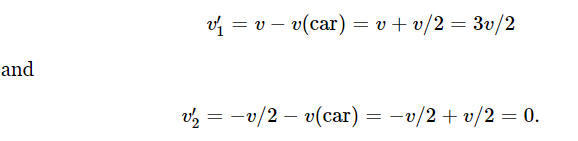
After the collision, the mass 3m appears to us to be moving with velocity v/2. Thus we have the answer, i.e., the ratio of velocities before and after collision is 3 to 1: if an object of mass m collides with a stationary object of mass 2m, then the whole thing moves off, stuck together, with a velocity 1/3 as much. The general rule again is that the sum of the products of the masses and the velocities stays the same: mv+0 equals 3m times v/3, so we are gradually building up the theorem of the conservation of momentum, piece by piece.

Now we have one against two. Using the same arguments, we can predict the result of one against three, two against three, etc. The case of two against three, starting from rest, is shown in Fig. 10–8.

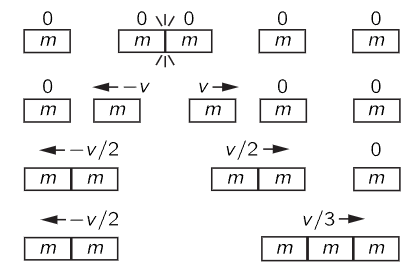
Fig. 10–8. Action and reaction between 2m and 3m.

In every case we find that the mass of the first object times its velocity, plus the mass of the second object times its velocity, is equal to the total mass of the final object times its velocity. These are all examples, then, of the conservation of momentum. Starting from simple, symmetrical cases, we have demonstrated the law for more complex cases. We could, in fact, do it for any rational mass ratio, and since every ratio is exceedingly close to a rational ratio, we can handle every ratio as precisely as we wish.

______________________________________________

Margin

1- H. V. Neher and R. B. Leighton, Amer. Jour. of Phys. 31, 255 (1963).

مواضيع ذات صلة

أنظمة لأكثر من جسيم واحد

كمية التحرك الزاوية والقوة المركزية

الحركة الدورانية

امثلة عن الاتزان الاستاتيكي للأجسام الممتدة

الاتزان الاستاتيكي للأجسام الممتدة

تعريف العزم

تذبذبات صغيرة لبندول

اعتبارات الطاقة في الحركة التوافقية البسيطة

الحل الهندسي للمعادلة التفاضلية للحركة التوافقية البسيطة، دائرة المرجع

الحل باستخدام حساب التفاضل والتكامل

قانون هوك والمعادلة التفاضلية للحركة التوافقية البسيطة

القدرة ووحدات الشغل