
Halley,s Irrational Formula
 المؤلف:
Ortega, J. M. and Rheinboldt, W. C.
المؤلف:
Ortega, J. M. and Rheinboldt, W. C.
 المصدر:
Iterative Solution of Nonlinear Equations in Several Variables. Philadelphia, PA: SIAM, 2000.
المصدر:
Iterative Solution of Nonlinear Equations in Several Variables. Philadelphia, PA: SIAM, 2000.
 الجزء والصفحة:
...
الجزء والصفحة:
...
 10-12-2021
10-12-2021
 1023
1023
Halley's Irrational Formula
A root-finding algorithm which makes use of a third-order Taylor series
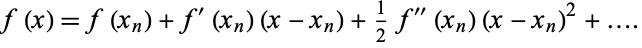 |
(1)
|
A root of 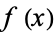 satisfies
satisfies 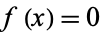 , so
, so
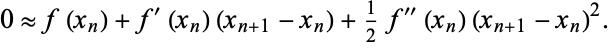 |
(2)
|
Using the quadratic equation then gives
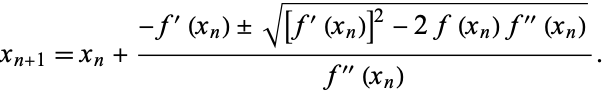 |
(3)
|
Picking the plus sign gives the iteration function
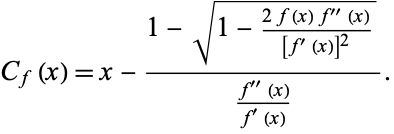 |
(4)
|
This equation can be used as a starting point for deriving Halley's method.
If the alternate form of the quadratic equation is used instead in solving (◇), the iteration function becomes instead
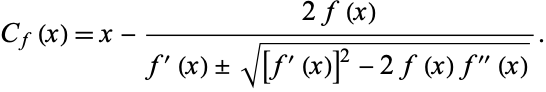 |
(5)
|
This form can also be derived by setting 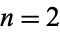 in Laguerre's method. Numerically, the sign in the denominator is chosen to maximize its absolute value. Note that in the above equation, if
in Laguerre's method. Numerically, the sign in the denominator is chosen to maximize its absolute value. Note that in the above equation, if 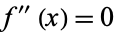 , then Newton's method is recovered. This form of Halley's irrational formula has cubic convergence, and is usually found to be substantially more stable than Newton's method. However, it does run into difficulty when both
, then Newton's method is recovered. This form of Halley's irrational formula has cubic convergence, and is usually found to be substantially more stable than Newton's method. However, it does run into difficulty when both 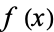 and
and 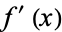 or
or 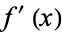 and
and 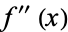 are simultaneously near zero.
are simultaneously near zero.
REFERENCES:
Gourdon, X. and Sebah, P. "Newton's Iteration." http://numbers.computation.free.fr/Constants/Algorithms/newton.html.
Ortega, J. M. and Rheinboldt, W. C. Iterative Solution of Nonlinear Equations in Several Variables. Philadelphia, PA: SIAM, 2000.
Qiu, H. "A Robust Examination of the Newton-Raphson Method with Strong Global Convergence Properties." Master's Thesis. University of Central Florida, 1993.
Scavo, T. R. and Thoo, J. B. "On the Geometry of Halley's Method." Amer. Math. Monthly 102, 417-426, 1995.
 الاكثر قراءة في التحليل العددي
الاكثر قراءة في التحليل العددي
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


