A-Sequence
المؤلف:
Erdős, P
المصدر:
"Remarks on Number Theory III. Some Problems in Additive Number Theory." Mat. Lapok 13
الجزء والصفحة:
...
22-10-2020
2291
A-Sequence
An infinite sequence of positive integers 
satisfying
 |
(1)
|
is an 
-sequence if no 
is the sum of two or more distinct earlier terms (Guy 1994). Such sequences are sometimes also known as sum-free sets.
Erdős (1962) proved
 |
(2)
|
Any 
-sequence satisfies the chi inequality (Levine and O'Sullivan 1977), which gives 
. Abbott (1987) and Zhang (1992) have given a bound from below, so the best result to date is
 |
(3)
|
Levine and O'Sullivan (1977) conjectured that the sum of reciprocals of an 
-sequence satisfies
 |
(4)
|
where 
are given by the Levine-O'Sullivan greedy algorithm. However, summing the first 
terms of the Levine-O'Sullivan sequence already gives 3.0254....
REFERENCES:
Abbott, H. L. "On Sum-Free Sequences." Acta Arith. 48, 93-96, 1987.
Erdős, P. "Remarks on Number Theory III. Some Problems in Additive Number Theory." Mat. Lapok 13, 28-38, 1962.
Finch, S. R. "Erdős' Reciprocal Sum Constants." §2.20 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 163-166, 2003.
Guy, R. K. "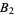
-Sequences." §E28 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 228-229, 1994.
Levine, E. and O'Sullivan, J. "An Upper Estimate for the Reciprocal Sum of a Sum-Free Sequence." Acta Arith. 34, 9-24, 1977.
Zhang, Z. X. "A Sum-Free Sequence with Larger Reciprocal Sum." Unpublished manuscript, 1992.
الاكثر قراءة في نظرية الاعداد
اخر الاخبار
اخبار العتبة العباسية المقدسة
