

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Prime Number Theorem
المؤلف:
Apostol, T. M
المصدر:
Introduction to Analytic Number Theory. New York: Springer-Verlag, 1976.
الجزء والصفحة:
...
26-8-2020
3557
Prime Number Theorem
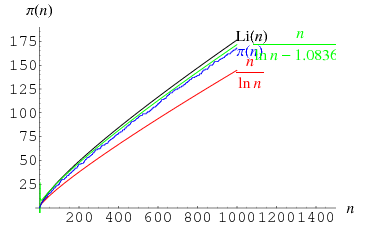
The prime number theorem gives an asymptotic form for the prime counting function 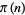 , which counts the number of primes less than some integer
, which counts the number of primes less than some integer 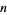 . Legendre (1808) suggested that for large
. Legendre (1808) suggested that for large 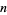 ,
,
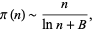 |
(1) |
with 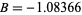 (where
(where 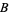 is sometimes called Legendre's constant), a formula which is correct in the leading term only,
is sometimes called Legendre's constant), a formula which is correct in the leading term only,
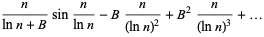 |
(2) |
(Nagell 1951, p. 54; Wagon 1991, pp. 28-29; Havil 2003, p. 177).
In 1792, when only 15 years old, Gauss proposed that
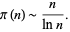 |
(3) |
Gauss later refined his estimate to
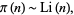 |
(4) |
where
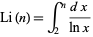 |
(5) |
is the logarithmic integral. Gauss did not publish this result, which he first mentioned in an 1849 letter to Encke. It was subsequently posthumously published in 1863 (Gauss 1863; Havil 2003, pp. 174-176).
Note that 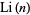 has the asymptotic series about
has the asymptotic series about 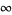 of
of
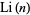 |
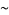 |
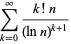 |
(6) |
 |
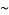 |
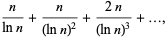 |
(7) |
and taking the first three terms has been shown to be a better estimate than 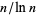 alone (Derbyshire 2004, pp. 116-117).
alone (Derbyshire 2004, pp. 116-117).
The statement (4) is often known as "the" prime number theorem and was proved independently by Hadamard (1896) and de la Vallée Poussin (1896). A plot of 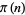 (lower curve) and
(lower curve) and 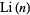 is shown above for
is shown above for 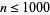 .
.
For small 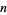 , it had been checked and always found that
, it had been checked and always found that 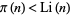 . As a result, many prominent mathematicians, including no less than both Gauss and Riemann, conjectured that the inequality was strict. To everyone's surprise, this conjecture was refuted when Littlewood (1914) proved that the inequality reverses infinitely often for sufficiently large
. As a result, many prominent mathematicians, including no less than both Gauss and Riemann, conjectured that the inequality was strict. To everyone's surprise, this conjecture was refuted when Littlewood (1914) proved that the inequality reverses infinitely often for sufficiently large 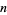 (Ball and Coxeter 1987; Havil 2003, p. 199). Skewes then showed that the first crossing of
(Ball and Coxeter 1987; Havil 2003, p. 199). Skewes then showed that the first crossing of 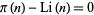 occurs before
occurs before  , a number now known as the Skewes number (Havil 2003, p. 199). The upper bound for the crossing has subsequently been reduced to
, a number now known as the Skewes number (Havil 2003, p. 199). The upper bound for the crossing has subsequently been reduced to 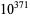 . Lehman (1966) proved that at least
. Lehman (1966) proved that at least 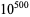 reversals occur for numbers with 1166 or 1167 decimal digits.
reversals occur for numbers with 1166 or 1167 decimal digits.
Chebyshev put limits on the ratio
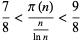 |
(8) |
(Landau 1927; Nagell 1951, p. 55; Landau 1974; Hardy and Wright 1979, Ch. 22; Ingham 1990; Rubinstein and Sarnak 1994; Hardy 1999, p. 27; Derbyshire 2004, pp. 124 and 154). For large 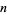 , he showed that
, he showed that
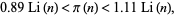 |
(9) |
where 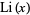 is the logarithmic integral (Edwards 2001, p. 4), and
is the logarithmic integral (Edwards 2001, p. 4), and
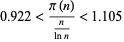 |
(10) |
(Havil 2003, p. 186). He also showed that if the limit
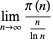 |
(11) |
exists, then it is 1 (Havil 2003, p. 186). Derbyshire's (2004, p. 124) statement that in 1850, Chebyshev also showed that 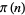 cannot differ from
cannot differ from 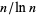 by more than approximately 10% is therefore correct only for sufficiently large
by more than approximately 10% is therefore correct only for sufficiently large 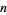 .
.
Hadamard and de la Vallée Poussin independently proved the prime number theorem in 1896 by showing that the Riemann zeta function 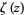 has no zeros of the form
has no zeros of the form 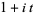 , in the sense that no deeper properties of
, in the sense that no deeper properties of 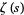 are required for the proof (Smith 1994, p. 128; Hardy 1999, pp. 58-60). Wiener (1951) allowed this somewhat vague statement to be interpreted literally (Hardy 1999, pp. 34 and 46), and this proof was simplified by Landau (1932) and Bochner (1933).
are required for the proof (Smith 1994, p. 128; Hardy 1999, pp. 58-60). Wiener (1951) allowed this somewhat vague statement to be interpreted literally (Hardy 1999, pp. 34 and 46), and this proof was simplified by Landau (1932) and Bochner (1933).
An elementary proof was found by Erdős (1949) and Selberg (1950) (Ball and Coxeter 1987, p. 63; Havil 2003, p. 188), although an unfortunate priority dispute over the joint work marred the otherwise beautiful proof (Hoffman 1998, pp. 39-41; Derbyshire 2004, p. 125). Versions of elementary proofs of the prime number theorem appear in final section of Nagell (1951) and in Hardy and Wright (1979, pp. 359-367). As noted by Hardy and Wright (1979, p. 9), although this proof is 'elementary,' "this proof is not easy."
Hadamard's proof depends on the simple trigonometric inequality
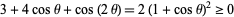 |
(12) |
(Hardy 1999, p. 58; Havil 2003, p. 187). de la Vallée Poussin (1899) showed that
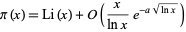 |
(13) |
for some constant 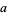 (Knuth 1998, p. 381), where
(Knuth 1998, p. 381), where 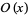 is asymptotic notation. In 1901, Koch showed that if the Riemann hypothesis is true, then
is asymptotic notation. In 1901, Koch showed that if the Riemann hypothesis is true, then
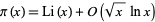 |
(14) |
(Havil 2003, p. 205), which can be written in the slightly weaker form
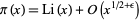 |
(15) |
(Derbyshire 2004, pp. 237 and 242-244).
The error term in (15) has subsequently been improved to
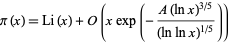 |
(16) |
(Walfisz 1963; Riesel 1994, p. 56; Knuth 1998, p. 382; Derbyshire 2004, p. 244). Ingham (1930) proved the prime number theorem using the identity of Ramanujan
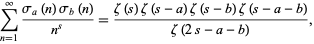 |
(17) |
where 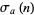 is the divisor function (Hardy 1999, pp. 59-60).
is the divisor function (Hardy 1999, pp. 59-60).
Riemann estimated the prime counting function with
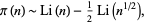 |
(18) |
which is a better approximation than 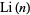 for
for 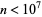 . Riemann (1859) also suggested the Riemann function
. Riemann (1859) also suggested the Riemann function
 |
(19) |
where 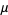 is the Möbius function (Wagon 1991, p. 29). An even better approximation for small
is the Möbius function (Wagon 1991, p. 29). An even better approximation for small 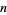 (by a factor of 10 for
(by a factor of 10 for 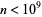 ) is the Gram series.
) is the Gram series.
The prime number theorem is equivalent to either
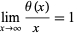 |
(20) |
or
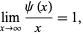 |
(21) |
where 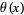 and
and 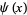 are the Chebyshev functions. Chebyshev showed that the only possible limit of these expressions was 1, but was not able to prove existence of the limit (Hardy 1999, p. 28).
are the Chebyshev functions. Chebyshev showed that the only possible limit of these expressions was 1, but was not able to prove existence of the limit (Hardy 1999, p. 28).
The Riemann hypothesis is equivalent to the assertion that
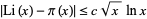 |
(22) |
for some value of 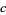 (Ingham 1990, p. 83; Landau 1974, pp. 378-388; Ball and Coxeter 1987; Hardy 1999, p. 26), as shown by Koch in 1901 (Havil 2003, p. 205). Some limits obtained without assuming the Riemann hypothesis are
(Ingham 1990, p. 83; Landau 1974, pp. 378-388; Ball and Coxeter 1987; Hardy 1999, p. 26), as shown by Koch in 1901 (Havil 2003, p. 205). Some limits obtained without assuming the Riemann hypothesis are
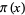 |
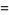 |
![Li(x)+O[xe^(-(lnx)^(1/2)/15)]](https://mathworld.wolfram.com/images/equations/PrimeNumberTheorem/Inline46.gif) |
(23) |
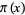 |
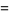 |
![Li(x)+O[xe^(-0.009(lnx)^(3/5)/(lnlnx)^(1/5))].](https://mathworld.wolfram.com/images/equations/PrimeNumberTheorem/Inline49.gif) |
(24) |
REFERENCES:
Apostol, T. M. Introduction to Analytic Number Theory. New York: Springer-Verlag, 1976.
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, pp. 62-64, 1987.
Berndt, B. C. Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, 1994.
Bochner. Math. Z. 37, 1-9, 1933.
Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, p. 64, 2003.
Courant, R. and Robbins, H. "The Prime Number Theorem." §1.2c in Supplement to Ch. 1 in What Is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, pp. 27-30, 1996.
Crandall, R. and Pomerance, C. Prime Numbers: A Computational Perspective, 2nd ed. New York: Springer-Verlag, 2005.
Davenport, H. "Prime Number Theorem." Ch. 18 in Multiplicative Number Theory, 2nd ed. New York: Springer-Verlag, pp. 111-114, 1980.
de la Vallée Poussin, C.-J. "Recherches analytiques la théorie des nombres premiers." Ann. Soc. scient. Bruxelles 20, 183-256, 1896.
Vallée Poussin, C. Mém. Couronnés Acad. Roy. Belgique 59, 1-74, 1899.
Derbyshire, J. "The Prime Number Theorem." Ch. 3 in Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York: Penguin, pp. 32-47, 2004.
Edwards, H. M. Riemann's Zeta Function. New York: Dover, 2001.
Erdős, P. "Démonstration élémentaire du théorème sur la distribution des nombres premiers." Scriptum 1, Centre Mathématique, Amsterdam, 1949.
Gauss, C. F. Werke, Band 10, Teil I. p. 10, 1863.
Hadamard, J. "Sur la distribution des zéros de la fonction 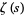 et ses conséquences arithmétiques (')." Bull. Soc. math. France 24, 199-220, 1896.
et ses conséquences arithmétiques (')." Bull. Soc. math. France 24, 199-220, 1896.
Hardy, G. H. "The Proof of the Prime Number Theorem" and "Second Approximation of the Proof." §2.5 and 2.6 in Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, pp. 16, 27, and 28-33, 1999.
Hardy, G. H. and Wright, E. M. "Statement of the Prime Number Theorem." §1.8 in An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, pp. 9-10, 1979.
Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, 2003.
Hoffman, P. The Man Who Loved Only Numbers: The Story of Paul Erdős and the Search for Mathematical Truth. New York: Hyperion, 1998.
Ingham, A. E. "Note on Riemann's 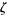 -Function and Dirichlet's
-Function and Dirichlet's 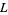 -Functions." J. London Math. Soc. 5, 107-112, 1930.
-Functions." J. London Math. Soc. 5, 107-112, 1930.
Ingham, A. E. The Distribution of Prime Numbers. London: Cambridge University Press, p. 83, 1990.
Knuth, D. E. The Art of Computer Programming, Vol. 2: Seminumerical Algorithms, 3rd ed. Reading, MA: Addison-Wesley, 1998.
Landau, E. Elementare Zahlentheorie. Leipzig, Germany: Hirzel, 1927. Reprinted Providence, RI: Amer. Math. Soc., 1990.
Landau, E. Berliner Sitzungsber., 514-521, 1932.
Landau, E. Vorlesungen über Zahlentheorie, Vol. 1. New York: Chelsea, pp. 79-96, 1970.
Landau, E. Handbuch der Lehre von der Verteilung der Primzahlen, 3rd ed. New York: Chelsea, 1974.
Legendre, A. M. Essai sur la Théorie des Nombres. Paris: Duprat, 1808.
Lehman, R. S. "On the Difference 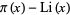 ." Acta Arith. 11, 397-410, 1966.
." Acta Arith. 11, 397-410, 1966.
Littlewood, J. E. "Sur les distribution des nombres premiers." Comptes Rendus Acad. Sci. Paris 158, 1869-1872, 1914.
Lu, W. C. "On the Elementary Proof of the Prime Number Theorem with a Remainder Term." Rocky Mountain J. Math. 29, 979, 1999.
Nagell, T. "The Prime Number Theorem." Ch. 8 in Introduction to Number Theory. New York: Wiley, pp. 275-299, 1951.
Riemann, G. F. B. "Über die Anzahl der Primzahlen unter einer gegebenen Grösse." Monatsber. Königl. Preuss. Akad. Wiss. Berlin, 671-680, Nov. 1859.
Reprinted in Das Kontinuum und Andere Monographen (Ed. H. Weyl). New York: Chelsea, 1972.
Riesel, H. "The Remainder Term in the Prime Number Theorem." Prime Numbers and Computer Methods for Factorization, 2nd ed. Boston, MA: Birkhäuser, p. 6, 1994.
Rubinstein, M. and Sarnak, P. "Chebyshev's Bias." Experimental Math. 3, 173-197, 1994.
Selberg, A. "An Elementary Proof of the Prime Number Theorem." Ann. Math. 50, 305-313, 1949.
Shanks, D. "The Prime Number Theorem." §1.6 in Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, pp. 15-17, 1993.
Smith, D. E. A Source Book in Mathematics. New York: Dover, 1994.
Wagon, S. Mathematica in Action. New York: W. H. Freeman, pp. 25-35, 1991.
Walfisz, A. Ch. 5 in Weyl'sche Exponentialsummen in der neueren Zahlentheorie. Berlin: Deutscher Verlag der Wissenschaften, 1963.
Wiener, N. §19 et seq. in The Fourier Integral and Certain of Its Applications. New York: Dover, 1951.
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















