Modular Prime Counting Function
المؤلف:
Derbyshire, J.
المصدر:
Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York: Penguin,
الجزء والصفحة:
...
26-8-2020
1263
Modular Prime Counting Function
By way of analogy with the prime counting function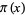 
, the notation 
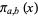denotes the number of primes of the form 
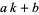less than or equal to 
(Shanks 1993, pp. 21-22).
Hardy and Littlewood proved that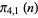 
an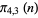 
switches leads infinitely often, a result known as the prime quadratic effect. The bias of the sign of 
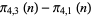is known as the Chebyshev bias.
Groups of equinumerous values of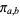 
include (
, 
), (
, 
), (
, 
, 
, 
), (
, 
), (
, 
, 
, 
, 
, 
), (
, 
, 
, 
), (
, 
, 
, 
, 
, 
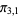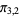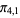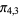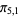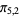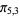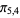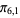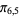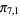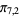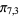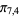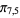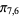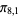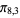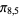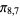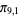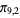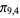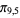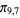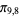), and so on. The values of 
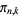for small 
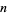are given in the following table for the first few powers of ten (Shanks 1993).
 |
 |
 |
 |
 |
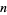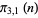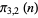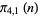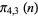| Sloane |
A091115 |
A091116 |
A091098 |
A091099 |
 |
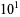1 |
2 |
1 |
2 |
 |
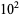11 |
13 |
11 |
13 |
 |
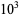80 |
87 |
80 |
87 |
 |
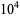611 |
617 |
609 |
619 |
 |
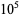4784 |
4807 |
4783 |
4808 |
 |
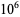39231 |
39266 |
39175 |
39322 |
 |
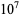332194 |
332384 |
332180 |
332398 |
 |
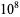2880517 |
2880937 |
2880504 |
2880950 |
 |
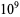25422713 |
25424820 |
25423491 |
25424042 |
 |
 |
 |
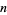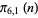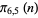| Sloane |
A091115 |
A091119 |
 |
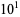1 |
1 |
 |
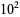11 |
12 |
 |
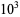80 |
86 |
 |
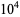611 |
616 |
 |
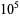4784 |
4806 |
 |
39231 |
39265 |
 |
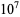332194 |
332383 |
 |
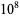2880517 |
2880936 |
 |
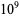25422713 |
25424819 |
 |
 |
 |
 |
 |
 |
 |
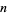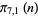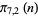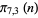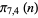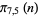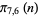| Sloane |
A091120 |
A091121 |
A091122 |
A091123 |
A091124 |
A091125 |
 |
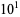0 |
1 |
1 |
0 |
1 |
0 |
 |
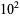3 |
4 |
5 |
3 |
5 |
4 |
 |
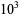28 |
27 |
30 |
26 |
29 |
27 |
 |
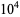203 |
203 |
209 |
202 |
211 |
200 |
 |
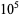1593 |
1584 |
1613 |
1601 |
1604 |
1596 |
 |
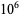13063 |
13065 |
13105 |
13069 |
13105 |
13090 |
 |
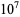110653 |
110771 |
110815 |
110776 |
110787 |
110776 |
 |
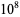960023 |
960114 |
960213 |
960085 |
960379 |
960640 |
 |
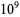8474221 |
8474796 |
8475123 |
8474021 |
8474630 |
8474742 |
 |
 |
 |
 |
 |
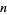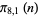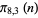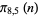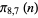| Sloane |
A091126 |
A091127 |
A091128 |
A091129 |
 |
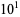0 |
1 |
1 |
1 |
 |
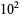5 |
7 |
6 |
6 |
 |
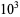37 |
44 |
43 |
43 |
 |
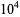295 |
311 |
314 |
308 |
 |
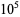2384 |
2409 |
2399 |
2399 |
 |
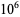19552 |
19653 |
19623 |
19669 |
 |
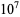165976 |
166161 |
166204 |
166237 |
 |
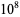1439970 |
1440544 |
1440534 |
1440406 |
 |
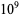12711220 |
12712340 |
12712271 |
12711702 |
Note that since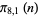 
, 
, 
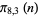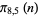, and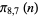 
are equinumerous,
are also equinumerous.
Erdős proved that there exist at least one prime of the form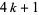 
and at least one prime of the form 
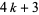between 
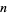and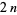 
for all 
.
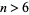REFERENCES:
Derbyshire, J. Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York: Penguin, p. 96, 2004.
Granville, A. and Martin, G. "Prime Number Races." Aug. 24, 2004. https://www.arxiv.org/abs/math.NT/0408319.
Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, 1993.
Sloane, N. J. A. Sequences A073505, A073506, A073508, A091098 A091099, A091115, A091116, A091117, A091119, A091120, A091121, A091122, A091123, A091124, and A091125 in "The On-Line Encyclopedia of Integer Sequences."
الاكثر قراءة في نظرية الاعداد
اخر الاخبار
اخبار العتبة العباسية المقدسة
