Lambert Series
المؤلف:
Abramowitz, M. and Stegun, I. A.
المصدر:
"Number Theoretic Functions." §24.3.1 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover
الجزء والصفحة:
...
24-8-2020
2693
Lambert Series
A Lambert series is a series of the form
 |
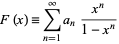(1)
|
for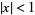 
. Then
where
 |
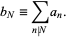(4)
|
The particular case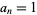 
is sometimes denoted
for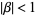 
(Borwein and Borwein 1987, pp. 91 and 95), where 
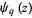is a q-polygamma function. Special cases and related sums include
(Borwein and Borwein 1997, pp. 91-92), which arise in the reciprocal Fibonacci and reciprocal Lucas constants.
Some beautiful series of this type include
where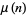 
is the Möbius function, 
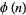is the totient function, 
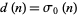is the number of divisors of 
, 
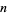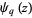is the q-polygamma function, 
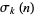is the divisor function, 
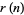is the number of representations of 
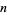in the form 
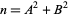where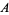 
and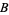 
are rational integers (Hardy and Wright 1979), 
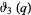is a Jacobi elliptic function (Bailey et al. 2006), 
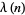is the Liouville function, and 
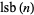is the least significant bit of 
.
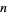REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Number Theoretic Functions." §24.3.1 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 826-827, 1972.
Apostol, T. M. Modular Functions and Dirichlet Series in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 24-15, 1997.
Arndt, J. "On Computing the Generalized Lambert Series." 24 Jun 2012. https://arxiv.org/abs/1202.6525.
Bailey, D. H.; Borwein, J. M.; Kapoor, V.; and Weisstein, E. W. "Ten Problems in Experimental Mathematics." Amer. Math. Monthly 113, 481-509, 2006.
Borwein, J. M. and Borwein, P. B. "Evaluation of Sums of Reciprocals of Fibonacci Sequences." §3.7 in Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, pp. 91-101, 1987.
Erdős, P. "On Arithmetical Properties of Lambert Series." J. Indian Math. Soc. 12, 63-66, 1948.
Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, pp. 257-258, 1979.
الاكثر قراءة في نظرية الاعداد
اخر الاخبار
اخبار العتبة العباسية المقدسة
