

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Zero
المؤلف:
Beeler, M. and Gosper, R. W. Item 57 in Beeler, M.; Gosper, R. W.; and Schroeppel, R.
المصدر:
HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239
الجزء والصفحة:
...
13-8-2020
3435
Zero
Zero is the integer denoted 0 that, when used as a counting number, means that no objects are present. It is the only integer (and, in fact, the only real number) that is neither negative nor positive. A number which is not zero is said to be nonzero. A root of a function  is also sometimes known as "a zero of
is also sometimes known as "a zero of  ."
."

The Schoolhouse Rock segment "My Hero, Zero" extols the virtues of zero with such praises as, "My hero, zero Such a funny little hero But till you came along We counted on our fingers and toes Now you're here to stay And nobody really knows How wonderful you are Why we could never reach a star Without you, zero, my hero How wonderful you are."
Zero is commonly taken to have the factorization 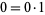 (e.g., in the Wolfram Language's FactorInteger[n] command). On the other hand, the divisors and divisor function
(e.g., in the Wolfram Language's FactorInteger[n] command). On the other hand, the divisors and divisor function 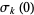 are generally taken to be undefined, since by convention,
are generally taken to be undefined, since by convention, 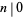 (i.e.,
(i.e., 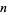 divides 0) for every
divides 0) for every 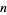 except zero.
except zero.
Because the number of permutations of 0 elements is 1, 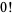 (zero factorial) is defined as 1 (Wells 1986, p. 31). This definition is useful in expressing many mathematical identities in simple form.
(zero factorial) is defined as 1 (Wells 1986, p. 31). This definition is useful in expressing many mathematical identities in simple form.
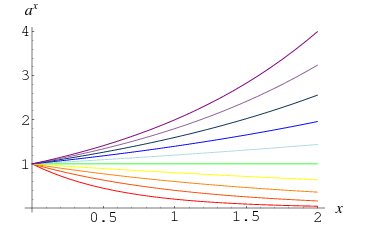
A number other than 0 taken to the power 0 is defined to be 1, which follows from the limit
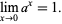 |
(1) |
This fact is illustrated by the convergence of curves at 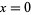 in the plot above, which shows
in the plot above, which shows 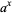 for
for 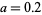 , 0.4, ..., 2.0. It can also be seen more intuitively by noting that repeatedly taking the square root of a number
, 0.4, ..., 2.0. It can also be seen more intuitively by noting that repeatedly taking the square root of a number 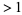 gives smaller and smaller numbers that approach one from above, while doing the same with a number between 0 and 1 gives larger and larger numbers that approach one from below. For
gives smaller and smaller numbers that approach one from above, while doing the same with a number between 0 and 1 gives larger and larger numbers that approach one from below. For 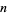 square roots, the total power taken is
square roots, the total power taken is 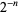 , which approaches 0 as
, which approaches 0 as 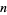 is large, giving
is large, giving 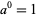 in the limit that
in the limit that 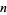 is large.
is large.
 itself is undefined. The lack of a well-defined meaning for this quantity follows from the mutually contradictory facts that
itself is undefined. The lack of a well-defined meaning for this quantity follows from the mutually contradictory facts that 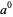 is always 1, so
is always 1, so 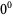 should equal 1, but
should equal 1, but  is always 0 (for
is always 0 (for  ), so
), so 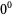 should equal 0. It could be argued that
should equal 0. It could be argued that  is a natural definition since
is a natural definition since
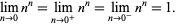 |
(2) |
However, the limit does not exist for general complex values of 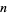 . Therefore, the choice of definition for
. Therefore, the choice of definition for  is usually defined to be indeterminate.
is usually defined to be indeterminate.
However, defining 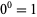 allows some formulas to be expressed simply (Knuth 1992; Knuth 1997, p. 57), an example of which is the beautiful analytical formula for the integral of the generalized sinc function
allows some formulas to be expressed simply (Knuth 1992; Knuth 1997, p. 57), an example of which is the beautiful analytical formula for the integral of the generalized sinc function
![int_0^infty(sin^ax)/(x^b)dx=(pi^(1-c)(-1)^(|_(a-b)/2_|))/(2^(a-c)(b-1)!)sum_(k=0)^(|_a/2_|-c)(-1)^k(a; k)(a-2k)^(b-1)[ln(a-2k)]^c](https://mathworld.wolfram.com/images/equations/Zero/NumberedEquation3.gif) |
(3) |
given by Kogan (cf. Espinosa and Moll 2000), where 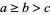 ,
,  , and
, and  is the floor function.
is the floor function.
Richardson's theorem is a fundamental result in decidability theory which establishes that the determination of whether even simple expressions are identically equal to zero is undecidable in principle, let alone in practice.
The following table gives the first few numbers  such that the decimal expansion of
such that the decimal expansion of  contains no zeros for small
contains no zeros for small 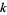 (a problem that resembles Gelfand's question.) The largest known
(a problem that resembles Gelfand's question.) The largest known  for which
for which  contain no zeros is 86 (Madachy 1979), with no other
contain no zeros is 86 (Madachy 1979), with no other  (M. Cook, pers. comm., Sep. 26, 1997 and Mar. 16, 1998), improving the
(M. Cook, pers. comm., Sep. 26, 1997 and Mar. 16, 1998), improving the  limit obtained by Beeler and Gosper (1972). The values
limit obtained by Beeler and Gosper (1972). The values 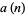 such that the positions of the rightmost zero in
such that the positions of the rightmost zero in 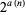 increases are 10, 20, 30, 40, 46, 68, 93, 95, 129, 176, 229, 700, 1757, 1958, 7931, 57356, 269518, ... (OEIS A031140). The positions in which the rightmost zeros occur are 2, 5, 8, 11, 12, 13, 14, 23, 36, 38, 54, 57, 59, 93, 115, 119, 120, 121, 136, 138, 164, ... (OEIS A031141). The rightmost zero of
increases are 10, 20, 30, 40, 46, 68, 93, 95, 129, 176, 229, 700, 1757, 1958, 7931, 57356, 269518, ... (OEIS A031140). The positions in which the rightmost zeros occur are 2, 5, 8, 11, 12, 13, 14, 23, 36, 38, 54, 57, 59, 93, 115, 119, 120, 121, 136, 138, 164, ... (OEIS A031141). The rightmost zero of  occurs at the 217th decimal place, the farthest over for powers up to
occurs at the 217th decimal place, the farthest over for powers up to  .
.
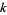 |
Sloane |  such that such that 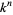 contains no 0s contains no 0s |
| 2 | A007377 | 1, 2, 3, 4, 5, 6, 7, 8, 9, 13, 14, 15, 16, 18, 19, 24, 25, 27, 28, ... |
| 3 | A030700 | 1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 12, 13, 14, 19, 23, 24, 26, 27, 28, ... |
| 4 | A030701 | 1, 2, 3, 4, 7, 8, 9, 12, 14, 16, 17, 18, 36, 38, 43, ... |
| 5 | A008839 | 1, 2, 3, 4, 5, 6, 7, 9, 10, 11, 17, 18, 30, 33, 58, ... |
| 6 | A030702 | 1, 2, 3, 4, 5, 6, 7, 8, 12, 17, 24, 29, 44, ... |
| 7 | A030703 | 1, 2, 3, 6, 7, 10, 11, 19, 35 |
| 8 | A030704 | 1, 2, 3, 5, 6, 8, 9, 11, 12, 13, 17, 24, 27 |
| 9 | A030705 | 1, 2, 3, 4, 6, 7, 12, 13, 14, 17, 34 |
| 11 | A030706 | 1, 2, 3, 4, 6, 7, 8, 9, 12, 13, 14, 15, 16, 18, 41, ... |
While it has not been proven that the numbers listed above are the only ones without zeros for a given base, the probability that any additional ones exist is vanishingly small. Under this assumption, the sequence of largest  such that
such that  contains no zeros for
contains no zeros for 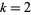 , 3, ... is then given by 86, 68, 43, 58, 44, 35, 27, 34, 0, 41, ... (OEIS A020665).
, 3, ... is then given by 86, 68, 43, 58, 44, 35, 27, 34, 0, 41, ... (OEIS A020665).
REFERENCES:
Beeler, M. and Gosper, R. W. Item 57 in Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239, p. 22, Feb. 1972. https://www.inwap.com/pdp10/hbaker/hakmem/number.html#item57.
Espinosa, O. and Moll, V. H. "On Some Definite Integrals Involving the Hurwitz Zeta Function." https://arxiv.org/abs/math/0012078. 11 Dec 2000.
Finch, S. R. Mathematical Constants. Cambridge, England: Cambridge University Press, 2003.
Knuth, D. E. "Two Notes on Notation." Amer. Math. Monthly 99, 403-422, 1992.
Knuth, D. E. The Art of Computer Programming, Vol. 1: Fundamental Algorithms, 3rd ed. Reading, MA: Addison-Wesley, p. 57, 1997.
Kogan, S. "A Note on Definite Integrals Involving Trigonometric Functions." Unpublished manuscript, n.d.
Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, pp. 127-128, 1979.
Pappas, T. "Zero-Where & When." The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, p. 162, 1989.
Schoolhouse Rock Site. "Multiplication Rock: 0 Zero My Hero." https://www.school-house-rock.com/0.html.
Sloane, N. J. A. Sequence A007377/M0485 in "The On-Line Encyclopedia of Integer Sequences."
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, pp. 23-26, 1986.
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















