تاريخ الرياضيات
الاعداد و نظريتها
تاريخ التحليل
تار يخ الجبر
الهندسة و التبلوجي
الرياضيات في الحضارات المختلفة
العربية
اليونانية
البابلية
الصينية
المايا
المصرية
الهندية
الرياضيات المتقطعة
المنطق
اسس الرياضيات
فلسفة الرياضيات
مواضيع عامة في المنطق
الجبر
الجبر الخطي
الجبر المجرد
الجبر البولياني
مواضيع عامة في الجبر
الضبابية
نظرية المجموعات
نظرية الزمر
نظرية الحلقات والحقول
نظرية الاعداد
نظرية الفئات
حساب المتجهات
المتتاليات-المتسلسلات
المصفوفات و نظريتها
المثلثات
الهندسة
الهندسة المستوية
الهندسة غير المستوية
مواضيع عامة في الهندسة
التفاضل و التكامل
المعادلات التفاضلية و التكاملية
معادلات تفاضلية
معادلات تكاملية
مواضيع عامة في المعادلات
التحليل
التحليل العددي
التحليل العقدي
التحليل الدالي
مواضيع عامة في التحليل
التحليل الحقيقي
التبلوجيا
نظرية الالعاب
الاحتمالات و الاحصاء
نظرية التحكم
بحوث العمليات
نظرية الكم
الشفرات
الرياضيات التطبيقية
نظريات ومبرهنات
علماء الرياضيات
500AD
500-1499
1000to1499
1500to1599
1600to1649
1650to1699
1700to1749
1750to1779
1780to1799
1800to1819
1820to1829
1830to1839
1840to1849
1850to1859
1860to1864
1865to1869
1870to1874
1875to1879
1880to1884
1885to1889
1890to1894
1895to1899
1900to1904
1905to1909
1910to1914
1915to1919
1920to1924
1925to1929
1930to1939
1940to the present
علماء الرياضيات
الرياضيات في العلوم الاخرى
بحوث و اطاريح جامعية
هل تعلم
طرائق التدريس
الرياضيات العامة
نظرية البيان
Figure Eight Knot
المؤلف:
Bailey, D. H.; Borwein, J. M.; Calkin, N. J.; Girgensohn, R.; Luke, D. R.; and Moll, V. H
المصدر:
Experimental Mathematics in Action. Wellesley, MA: A K Peters, 2007.
الجزء والصفحة:
...
24-2-2020
2140
+
-
20
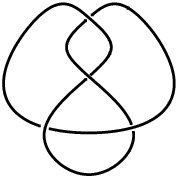
Figure Eight Knot
 |
 |
The figure eight knot, also known as the Flemish knot and savoy knot, is the unique prime knot of four crossings 04-001. It has braid word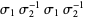 
.
The figure eight knot is implemented in the Wolfram Language as KnotData["FigureEight"].
It is a 2-embeddable knot, and is amphichiral as well as invertible. It has Arf invariant 1. It is not a slice knot (Rolfsen 1976, p. 224).
The Alexander polynomial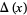 
, BLM/Ho polynomial 
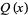, Conway polynomial 
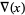, HOMFLY polynomial 
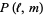, Jones polynomial 
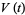, and Kauffman polynomial F 
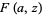of the figure eight knot are
 |
 |
 |
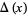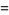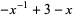(1) |
 |
 |
 |
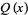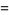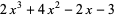(2) |
 |
 |
 |
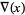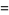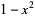(3) |
 |
 |
 |
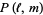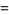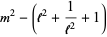(4) |
 |
 |
 |
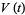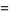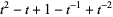(5) |
 |
 |
 |
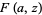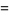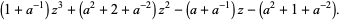(6) |
There are no other knots on 10 or fewer crossings sharing the same Alexander polynomial, BLM/Ho polynomial, bracket polynomial, HOMFLY polynomial, Jones polynomial, or Kauffman polynomial F.
The figure eight knot has knot group
 |
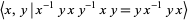(7) |
(Rolfsen 1976, p. 58).
Helaman Ferguson's sculpture "Figure-Eight Complement II" illustrates the knot complement of the figure eight knot (Borwein and Bailey 2003, pp. 54-55, color plate IV, and front cover; Bailey et al. 2007, p. 37). Furthermore, Ferguson has carved the BBP-type formula for the hyperbolic volume of the knot complement (discussed below) on both figure eight knot complement sculptures commissioned by the Clay Mathematics Institute (Borwein and Bailey 2003, p. 56; Bailey et al. 2007, pp. 36-38).
The hyperbolic volume of the knot complement of the figure eight knot is approximately given by
 |
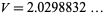(8) |
(OEIS A091518). Exact expressions are given by the infinite sums
 |
 |
 |
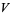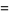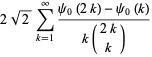(9) |
 |
 |
 |
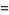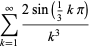(10) |
 |
 |
 |
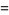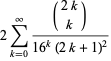(11) |
 |
 |
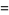![(2pi)/3[1-ln(pi/3)+sum_(k=1)^(infty)(zeta(2k))/(k(2k+1)6^(2k))]](http://mathworld.wolfram.com/images/equations/FigureEightKnot/Inline37.gif) |
(12) |
 |
 |
 |
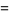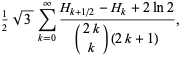(13) |
where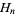 
is a harmonic number.
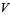has a variety of BBP-type formulas including
 |
 |
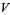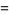![sqrt(3)sum_(k=0)^(infty)[1/((3k+1)^2)-2/((3k+2)^2)+4/((3k+3)^2)]](http://mathworld.wolfram.com/images/equations/FigureEightKnot/Inline45.gif) |
(14) |
 |
 |
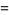![(3sqrt(3))/2sum_(k=0)^(infty)[1/((3k+1)^2)-1/((3k+2)^2)]](http://mathworld.wolfram.com/images/equations/FigureEightKnot/Inline48.gif) |
(15) |
 |
 |
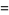![sqrt(3)sum_(k=0)^(infty)[1/((6k+1)^2)+1/((6k+2)^2)-1/((6k+4)^2)-1/((6k+5)^2)]](http://mathworld.wolfram.com/images/equations/FigureEightKnot/Inline51.gif) |
(16) |
 |
 |
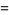![sqrt(3)sum_(k=0)^(infty)[2/((6k+1)^2)-3/((6k+2)^2)-1/((6k+5)^2)]](http://mathworld.wolfram.com/images/equations/FigureEightKnot/Inline54.gif) |
(17) |
 |
 |
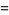![sqrt(3)sum_(k=0)^(infty)[1/((6k+1)^2)+3/((6k+4)^2)-2/((6k+5)^2)],](http://mathworld.wolfram.com/images/equations/FigureEightKnot/Inline57.gif) |
(18) |
with additional identities for coefficients of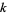 
of the form 
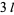(E. W. Weisstein, Sep. 30, 2007). Higher-order identities are
![V=(2sqrt(3))/(243)sum_(k=0)^infty1/(729^k)[(243)/((12k+1)^2)-(243)/((12k+2)^2)-(324)/((12k+3)^2)-(81)/((12k+4)^2)+(27)/((12k+5)^2)-9/((12k+7)^2)+9/((12k+8)^2)
+(12)/((12k+9)^2)+3/((12k+10)^2)-1/((12k+11)^2)]
=(2sqrt(3))/(177147)sum_(k=0)^infty1/(531441^k)[(177147)/((24k+1)^2)-(177147)/((24k+2)^2)-(236196)/((24k+3)^2)-(59049)/((24k+4)^2)+(19683)/((24k+5)^2)-(6561)/((24k+7)^2)+(6561)/((24k+8)^2)+(8748)/((24k+9)^2)+(2187)/((24k+10)^2)-(729)/((24k+11)^2)+(243)/((24k+13)^2)-(243)/((24k+14)^2)-(324)/((24k+15)^2)-(81)/((24k+16)^2)+(27)/((24k+17)^2)-9/((24k+19)^2)+9/((24k+20)^2)+(12)/((24k+21)^2)+3/((24k+22)^2)
-1/((24k+23)^2)]](http://mathworld.wolfram.com/images/equations/FigureEightKnot/NumberedEquation3.gif) |
(19) |
(E. W. Weisstein, Aug. 11, 2008).
Additional classes of identities are given by
 |
 |
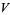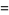![sqrt(3)sum_(k=0)^(infty)(-1)^k[1/((3k+1)^2)+1/((3k+2)^2)]](http://mathworld.wolfram.com/images/equations/FigureEightKnot/Inline62.gif) |
(20) |
 |
 |
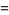![sqrt(3)sum_(k=0)^(infty)(-1)^k[1/((9k+1)^2)+1/((9k+2)^2)-1/((9k+4)^2)-1/((9k+5)^2)+1/((9k+7)^2)+1/((9k+8)^2)],](http://mathworld.wolfram.com/images/equations/FigureEightKnot/Inline65.gif) |
(21) |
with additional identities for coefficients of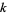 
of the form 
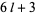(E. W. Weisstein, Sep. 30, 2007). Another BBP-type formula is given by
 |
 |
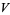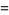![(2sqrt(3))/9sum_(k=0)^(infty)((-1)^k)/(27^k)[9/((6k+1)^2)-9/((6k+2)^2)-(12)/((6k+3)^2)-3/((6k+4)^2)+1/((6k+5)^2)].](http://mathworld.wolfram.com/images/equations/FigureEightKnot/Inline70.gif) |
(22) |
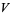is also given by the integrals
 |
 |
 |
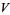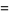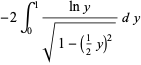(23) |
 |
 |
 |
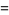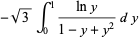(24) |
 |
 |
 |
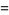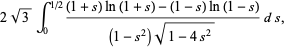(25) |
and the analytic expressions
 |
 |
 |
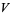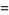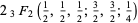(26) |
 |
 |
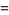![1/6sqrt(3)[psi_1(1/3)-psi_1(2/3)]](http://mathworld.wolfram.com/images/equations/FigureEightKnot/Inline86.gif) |
(27) |
 |
 |
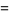![1/9sqrt(3)[3psi_1(1/3)-2pi^2]](http://mathworld.wolfram.com/images/equations/FigureEightKnot/Inline89.gif) |
(28) |
 |
 |
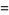![1/(36)sqrt(3)[psi_1(1/6)+psi_1(1/3)-psi_1(2/3)-psi_1(5/6)]](http://mathworld.wolfram.com/images/equations/FigureEightKnot/Inline92.gif) |
(29) |
 |
 |
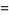![i[Li_2(e^(-ipi/3))-Li_2(e^(ipi/3))]](http://mathworld.wolfram.com/images/equations/FigureEightKnot/Inline95.gif) |
(30) |
 |
 |
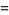![2I[Li_2(e^(ipi/3))]](http://mathworld.wolfram.com/images/equations/FigureEightKnot/Inline98.gif) |
(31) |
 |
 |
 |
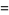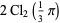(32) |
 |
 |
 |
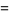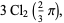(33) |
(Broadhurst 1998; Borwein and Bailey 2003, pp. 54 and 88-92; Bailey et al. 2007, pp. 36-38 and 265-266), where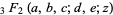 
is a generalized hypergeometric function, 
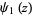is the trigamma function, 
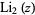is the dilogarithm and 
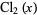is Clausen's integral.
REFERENCES:
Bailey, D. H.; Borwein, J. M.; Calkin, N. J.; Girgensohn, R.; Luke, D. R.; and Moll, V. H. Experimental Mathematics in Action. Wellesley, MA: A K Peters, 2007.
Bar-Natan, D. "The Knot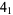 
." http://www.math.toronto.edu/~drorbn/KAtlas/Knots/4.1.html.
Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, 2003.
Broadhurst, D. J. "Massive 3-Loop Feynman Diagrams Reducible to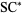 
Primitives of Algebras of the Sixth Root of Unity." March 11, 1998. http://arxiv.org/abs/hep-th/9803091.
Francis, G. K. A Topological Picture Book. New York: Springer-Verlag, 1987.
Kauffman, L. Knots and Physics. Teaneck, NJ: World Scientific, pp. 8, 12, and 35, 1991.
KnotPlot. "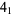
." http://newweb.cecm.sfu.ca/cgi-bin/KnotPlot/KnotServer/kserver?ncomp=1&ncross=4&id=1.
Livingston, C. Knot Theory. Washington, DC: Math. Assoc. Amer., pp. 21 and 153, 1993.
Owen, P. Knots. Philadelphia, PA: Courage, p. 16, 1993.
Rolfsen, D. Knots and Links. Wilmington, DE: Publish or Perish Press, pp. 58 and 224, 1976.
Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. Middlesex, England: Penguin Books, pp. 78-79, 1991.
الاكثر قراءة في نظرية الاعداد
اخر الاخبار
اخبار العتبة العباسية المقدسة
الآخبار الصحية
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
