Monstrous Moonshine
المؤلف:
Borcherds, R. E.
المصدر:
"Monstrous Moonshine and Monstrous Lie Superalgebras." Invent. Math. 109
الجزء والصفحة:
...
25-12-2019
977
Monstrous Moonshine
In 1979, Conway and Norton discovered an unexpected intimate connection between the monster group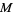 
and the j-function. The Fourier expansion of 
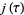is given by
 |
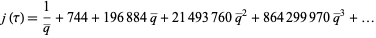(1)
|
(OEIS A000521), where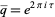 
and 
is the half-period ratio, and the dimensions of the first few irreducible representations of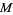 
are 1, 196883, 21296876, 842609326, ... (OEIS A001379).
In November 1978, J. McKay noticed that the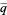 
-coefficient 196884 is exactly one more than the smallest dimension of nontrivial representations of the 
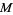(Conway and Norton 1979). In fact, it turns out that the Fourier coefficients of 
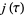can be expressed as linear combinations of these dimensions with small coefficients as follows:
Borcherds (1992) later proved this relationship, which became known as monstrous moonshine. Amazingly, there turn out to be yet more deep connections between the monster group and the j-function.
REFERENCES:
Borcherds, R. E. "Monstrous Moonshine and Monstrous Lie Superalgebras." Invent. Math. 109, 405-444, 1992.
Conway, J. H. and Norton, S. P. "Monstrous Moonshine." Bull. London Math. Soc. 11, 308-339, 1979.
Sloane, N. J. A. Sequences A000521/M5477 and A001379 in "The On-Line Encyclopedia of Integer Sequences."
الاكثر قراءة في نظرية الاعداد
اخر الاخبار
اخبار العتبة العباسية المقدسة
