Lamé,s Differential Equation
المؤلف:
Byerly, W. E
المصدر:
An Elementary Treatise on Fourier,s Series, and Spherical, Cylindrical, and Ellipsoidal Harmonics, with Applications to Problems in Mathematical Physics. New York: Dover, 1959.
الجزء والصفحة:
...
13-6-2018
1988
Lamé's Differential Equation
The ordinary differential equation
![(x^2-b^2)(x^2-c^2)(d^2z)/(dx^2)+x(x^2-b^2+x^2-c^2)(dz)/(dx)-[m(m+1)x^2-(b^2+c^2)p]z=0.](http://mathworld.wolfram.com/images/equations/LamesDifferentialEquation/NumberedEquation1.gif) |
(1)
|
(Byerly 1959, p. 255). The solution is denoted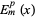 
and is known as an ellipsoidal harmonic of the first kind, or Lamé function. Whittaker and Watson (1990, pp. 554-555) give the alternative forms
(Whittaker and Watson 1990, pp. 554-555; Ward 1987; Zwillinger 1997, p. 124). Here,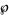 
is a Weierstrass elliptic function, 
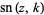is a Jacobi elliptic function, and
Two other equations named after Lamé are given by
 |
(10)
|
and
 |
(11)
|
(Moon and Spencer 1961, p. 157; Zwillinger 1997, p. 124).
REFERENCES:
Byerly, W. E. An Elementary Treatise on Fourier's Series, and Spherical, Cylindrical, and Ellipsoidal Harmonics, with Applications to Problems in Mathematical Physics. New York: Dover, 1959.
Moon, P. and Spencer, D. E. Field Theory for Engineers. New York: Van Nostrand, 1961.
Ward, R. S. "The Nahm Equations, Finite-Gap Potentials and Lamé Functions." J. Phys. A: Math. Gen. 20, 2679-2683, 1987.
Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, 1990.
Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, p. 124, 1997.
الاكثر قراءة في معادلات تفاضلية
اخر الاخبار
اخبار العتبة العباسية المقدسة
