
Simplicial Complexes-Geometrical Independence
 المؤلف:
David R. Wilkins
المؤلف:
David R. Wilkins
 المصدر:
Algebraic Topology
المصدر:
Algebraic Topology
 الجزء والصفحة:
...
الجزء والصفحة:
...
 25-6-2017
25-6-2017
 1773
1773
Definition Points v0, v1, . . . , vq in some Euclidean space Rk are said to be geometrically independent (or affine independent) if the only solution of the linear system

is the trivial solution λ0 = λ1 = · · · = λq = 0.
It is straightforward to verify that v0, v1, . . . , vq are geometrically independent if and only if the vectors v1 − v0, v2 − v0, . . . , vq − v0 are linearly independent. It follows from this that any set of geometrically independent points in Rk has at most k + 1 elements. Note also that if a set consists of geometrically independent points in Rk, then so does every subset of that set.
Definition A q-simplex in Rk is defined to be a set of the form
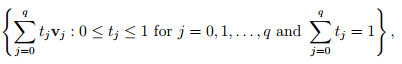
where v0, v1, . . . , vq are geometrically independent points of Rk. The points v0, v1, . . . , vq are referred to as the vertices of the simplex. The non-negative integer q is referred to as the dimension of the simplex.
Note that a 0-simplex in Rk is a single point of Rk, a 1-simplex in Rk is a line segment in Rk , a 2-simplex is a triangle, and a 3-simplex is a tetrahedron.
Let σ be a q-simplex in Rk with vertices v0, v1, . . . , vq. If x is a point of σ then there exist real numbers t0, t1, . . . , tq such that
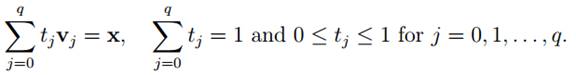
Moreover t0, t1, . . . , tq are uniquely determined:
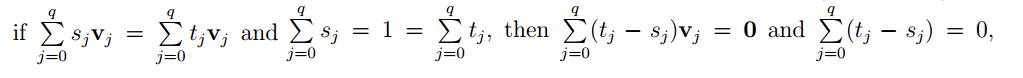
Hence tj − sj = 0 for all j, since v0, v1, . . . , vq are geometrically independent. We refer to t0, t1, . . . , tq as the barycentric coordinates of the point x of σ.
Lemma 1.1 Let q be a non-negative integer, let σ be a q-simplex in Rm, and let τ be a q-simplex in Rn, where m ≥ q and n ≥ q. Then σ and τ are homeomorphic.
Proof Let v0, v1, . . . , vq be the vertices of σ, and let w0, w1, . . . , wq be the vertices of τ . The required homeomorphism h: σ → τ is given by
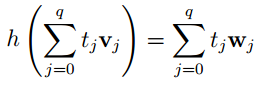
for all t0, t1, . . . , tq satisfying 0 ≤ tj ≤ 1 for j = 0, 1, . . . , q and
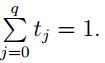
A homeomorphism between two q-simplices defined as in the above proof is referred to as a simplicial homeomorphism.
 الاكثر قراءة في التبلوجيا
الاكثر قراءة في التبلوجيا
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


