Accelerated frames of reference, equivalence principle and Einstein’s field equation

An observer who measures the acceleration of a freely falling body within a sufficiently small laboratory obtains the same results whether his/her laboratory is at rest in a gravitational field or appropriately accelerated in gravity-free space. Consequently, the quantity representing the inertial forces in the equation of motion should be similar to the quantity representing the gravitational forces. In an inertial frame in Cartesian coordinates x^μ, a force-free test particle obeys the equation of motion

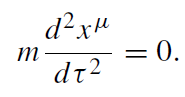 (1.1)

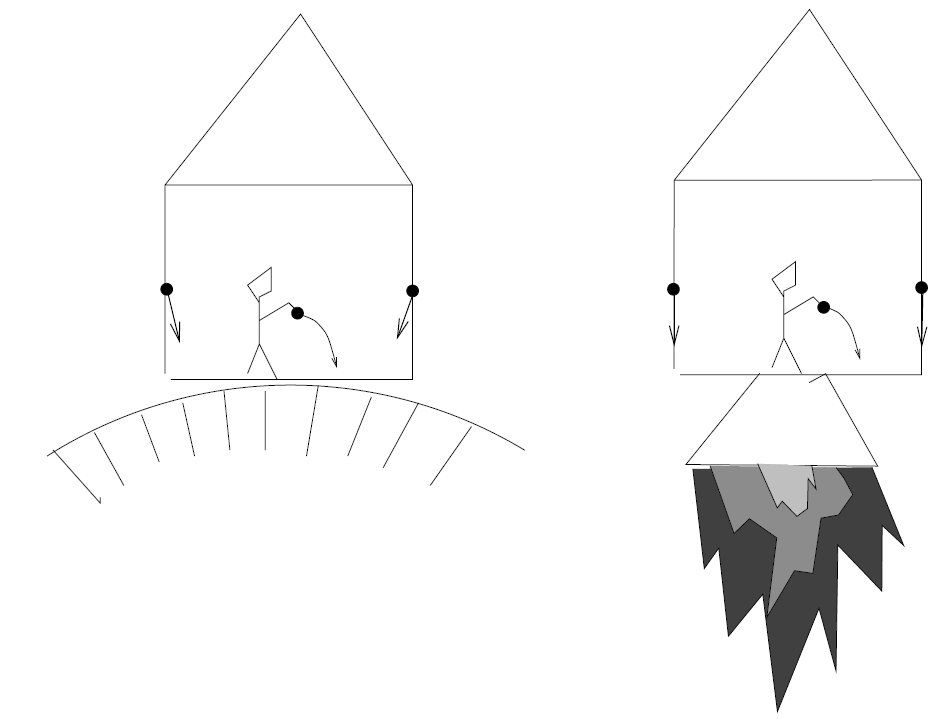
Figure 1.5. The local equivalence of an accelerated frame of reference and a gravitational field. Note, if we compare the gravitational and the inertial forces acting on two point particles in each case, because of the tidal effect, we can distinguish the laboratory on earth and that in space. However, locally, one test particle moves in the same way in both laboratories.

Thus it moves in a straight line x^μ(τ ) = a^μ+b^μτ (a^μ, b^μ constant vectors). The space laboratory represents an accelerated frame of reference with coordinates     x^μ'. We apply a coordinate transformation x^α' (x^μ) to (1.1) and find

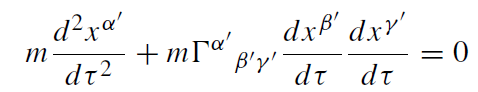 (1.2)

where the connection components

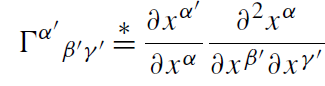 (1.3)

represent the inertial field. For a rotating coordinate system, e.g. encompasses the Coriolis force etc. So far Γ^α'_β'γ' is only an coordinate artifact and has no degrees of freedom of its own. We can always introduce a global coordinate system such that the Γ^α'_β'γ' vanish everywhere.

We can deduce an alternative representation of Γ^α'_β'γ' from the tensorial transformation behavior of the metric tensor (we suppress the dashes here):

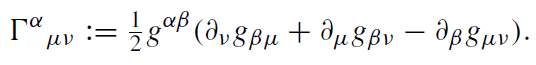 (1.4)

Thus, the connection components, also called the Christoffel symbols in the case of a Riemannian space, can be expressed in terms of ten functions g_αβ = g_βα which tentatively serve as the gravitational or inertial potential. In order to be able to choose a coordinate system such that Γ^α'_β'γ' = 0 globally, the Γ^α_βγ have to fulfil a certain integrability condition, namely their ‘curl’ has to vanish:

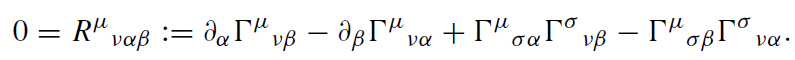 (1.5)

The quantity R^α_βμν is called the Riemannian curvature tensor. If R^α_βμν = 0, we have a flat Minkowski spacetime (possibly in curvilinear coordinates), whereas R^α_βμν ≠ 0 implies a curved Riemannian spacetime. In a Riemannian space, the curvature tensor fulfills certain algebraic identities which reduce its number of independent components to 20:

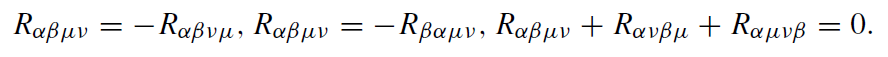 (1.6)

Let us now construct the field equation for gravity by trying to proceed along the same line as in other successful field theories, such as electrodynamics. The equations of motion with the abbreviation (^.) = d/dτ read:

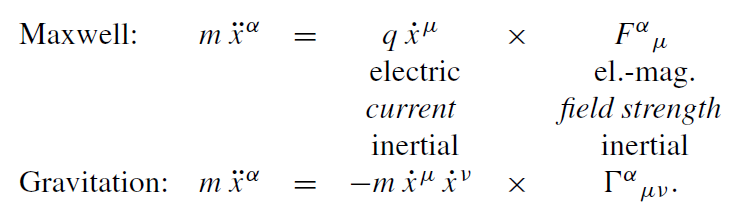 (1.7)

This fits quite nicely into our considerations in the previous section. The current, which couples to the inertial field, is the quantity m ẋ^μ ẋ^ν which corresponds to the energy–momentum tensor of dust T ^αβ = ρ ẋ^α ẋ^β. This coincides with the earlier suggestion that T ^αβ should be the source of gravity.

In electrodynamics, we have the four-potential Aμ = (φ_elec, A), φ_elec is the 3D scalar electric potential, A the 3D vector potential. Furthermore, the electromagnetic field strength is denoted by F_αβ = ∂_α A_β −∂_β A_α and the current by J ^α. With the Lorenz gauge, ∂_μ A^μ = 0, we find that

divergence of field ∼ d’Alembertian on potential ∼ source current

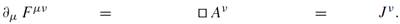 (1.8)

However, it is not so simple in gravity. Gravitational radiation carries energy, and energy is, as we have argued earlier, itself a source of gravity. Thus, the gravitational field has a self-interaction which distinguishes it from the electromagnetic field. Consequently, gravity is described by a nonlinear field equation of the following type:

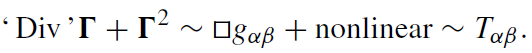 (1.9)

That the nonlinearity is only quadratic will be a result of our subsequent considerations.

So much for the general outline. To fix an exact equation, we need some additional criteria. In particular, we have to say something about general covariance. We consider an accelerated frame of reference locally equivalent to one which is at rest in a gravitational field. Gravity is a relatively weak force, but it has an infinite range and is all pervading. We will hardly find a gravity-free spot in the universe. Hence, in general we find ourselves in a non-inertial frame, even if the deviation from an inertial system may be negligible on small scales. From this point of view, the fundamental laws of physics should be covariant not only under Poincar'e transformations but also under general coordinate transformations. There is not much change with respect to the algebra of tensors, but a very noticeable change comes about in tensor analysis: the partial derivative of a tensor will not transform like a tensor. This can be fixed by introducing the so-called covariant derivative:

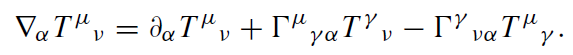 (1.10)

By replacing the partial derivatives in the special relativistic formulae by covariant ones, we obtain general covariant equations. This ‘correspondence’ principle mostly, but not always, yields physical reasonable generalizations of the special relativistic laws.

In Newton's theory, the mass density as source is linearly related to the tidal force. Can we also define tidal forces in general relativity?

            The equation of motion (1.1) has a geometrical interpretation, too. The metric allows the definition of an invariant length of a curve γ , parametrized by x_μ = x_μ(τ ), connecting two spacetime points A = x_μ(0) and B = x_μ(τ₀) by means of the line integral

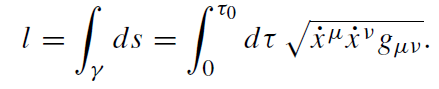 (1.11)

This length l represents the proper time of an observer who moves along the path γ from A to B. The necessary and sufficient condition for γ to be a curve of extremal length is found to be (provided γ is parametrized by its arc length)

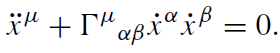 (1.12)

This is the Euler–Lagrange equation for the variational problem δʃ ds = 0; and it coincides with the equation of motion (1.1). In geometry, (1.12) is called the geodesic equation and its solutions x^μ are geodesics. In flat space, the geodesics are straight lines, the geodesics of a sphere are circuits, etc.

Thus, freely falling particles move along the geodesics of Riemannian spacetime. Now we can address the question of tidal accelerations between two freely falling particles. Let the vector v^μ be the vector describing the distance between two particles moving on infinitesimally adjacent geodesics. A simple calculation yields the equation for the geodesic deviation:

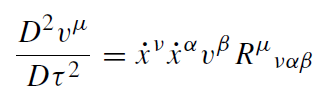 (1.13)

where D/Dτ denotes the absolute derivative along the curve x^α. Eventually, the tidal acceleration is represented by the curvature tensor. In Newton's theory, the tidal force is linearly related to the tidal acceleration. The energy–momentum tensor, as the suspected source of gravity, is a symmetric second-rank tensor. Therefore it has ten independent components.

Now only the problem of how to interrelate the second-rank symmetric energy–momentum tensor to the fourth-rank Riemannian curvature tensor remains. In analogy to the Newtonian case we would like this relation to be linear. It turns out that such a relation has to be of the form

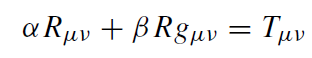 (1.14)

with the Ricci tensor

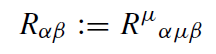 (1.15)

and the curvature scalar

 (1.16)

The constants α and β have to be fixed by additional conditions. The vanishing divergence of the energy–momentum together with the second Bianchi identity (a kind of integrability condition)

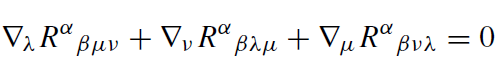 (1.17)

leads to Einstein’s field equation:

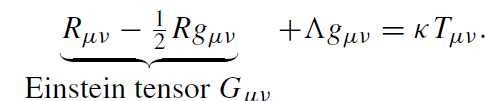 (1.18)

The value κ := 8πG/c4 of Einstein’s gravitational constant can be determined by a transition to the Newtonian limit of general relativity. Moreover, we have added a cosmological term containing the cosmological constant Λ.

The energy–momentum tensor has ten independent components whereas the Riemannian curvature tensor has 20 independent components. Hence, the energy– momentum tensor determines only a part of the curvature. Indeed, we have the decomposition

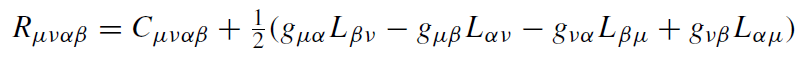 (1.19)

where

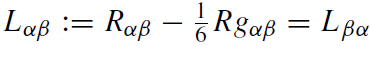 (1.20)

(for recent work on the L-tensor). This part of the curvature is algebraically linked to the matter distribution by means of Einstein’s equation. Consequently, it vanishes in vacuum and only the irreducible fourth-rank part C_{αβγ δ} , the conformal Weyl curvature with ten independent components, remains.