Separation of variables

The method of images and complex analysis are two rather elegant techniques for solving Poisson's equation. Unfortunately, they both have an extremely limited range of application. The final technique we shall discuss in this course, namely, the separation of variables, is somewhat messy but possess a far wider range of application. Let us examine a specific example. Consider two semi-infinite, grounded, conducting plates lying parallel to the x-z plane, one at y = 0, and the other at y = π. The left end, at x = 0, is closed off by an infinite strip insulated from the two plates and maintained at a specified potential ϕ₀(y). What is the potential in the region between the plates?

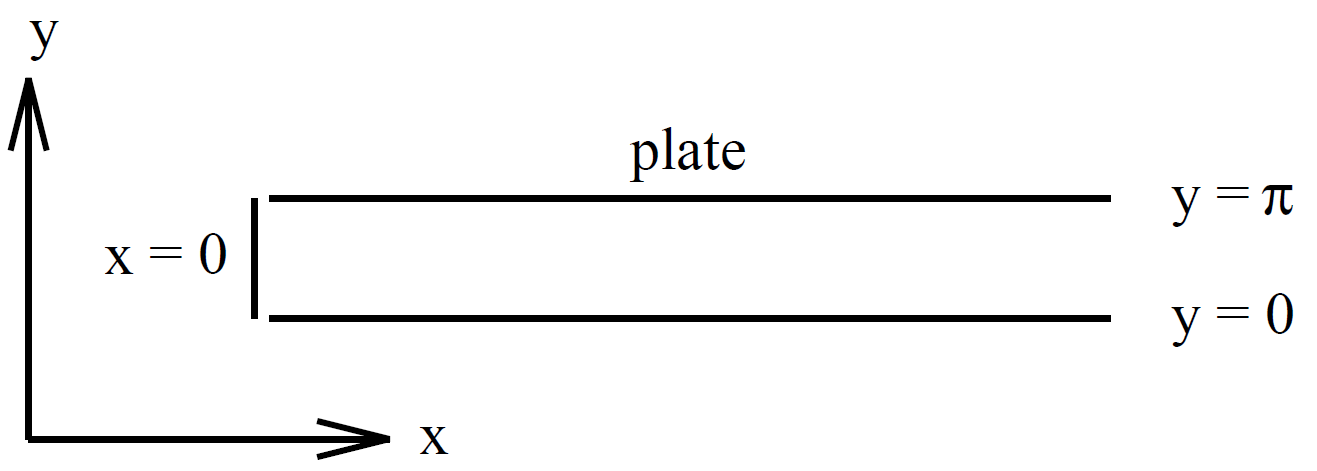
We first of all assume that the potential is z-independent, since everything else in the problem is. This reduces the problem to two dimensions. Poisson's equation is written

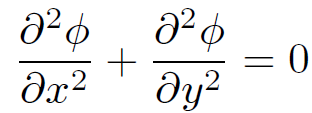 (1.1)

in the vacuum region between the conductors. The boundary conditions are

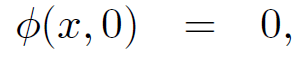 (1.2a)

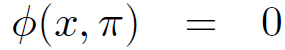 (1.2b)

for x > 0, since the two plates are earthed, plus

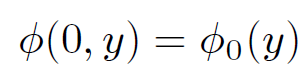 (1.3)

for 0 ≤ y ≤ π, and

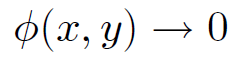 (1.4)

as x → ∞. The latter boundary condition is our usual one for the scalar potential at infinity. The central assumption in the method of separation of variables is that a multi-dimensional potential can be written as the product of one-dimensional potentials, so that

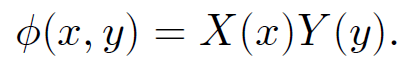 (1.5)

The above solution is obviously a very special one, and is, therefore, only likely to satisfy a very small subset of possible boundary conditions. However, it turns out that by adding together lots of different solutions of this form we can match to general boundary conditions. Substituting (1.5) into (1.1), we obtain

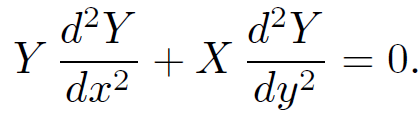 (1.6)

Let us now separate the variables; i.e., let us collect all of the x-dependent terms on one side of the equation, and all of the y-dependent terms on the other side. Thus,

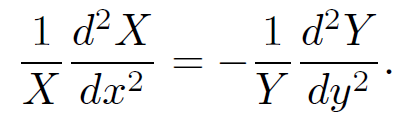 (1.7)

This equation has the form

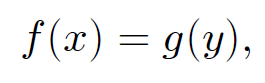 (1.8)

where f and g are general functions. The only way in which the above equation can be satisfied, for general x and y, is if both sides are equal to the same constant. Thus,

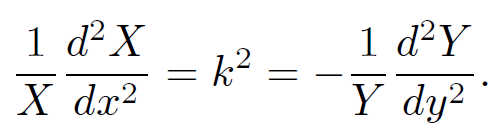 (1.9)

The reason why we write k², rather than -k², will become apparent later on. Equation (1.9) separates into two ordinary differential equations:

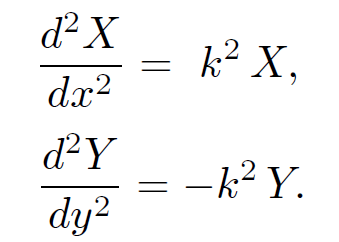 (1.10)

We know the general solution to these equations:

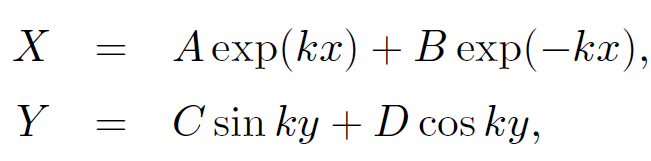 (1.11)

giving

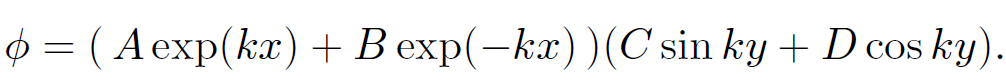 (1.12)

Here, A, B, C, and D are arbitrary constants. The boundary condition (1.4) is automatically satisfied if A = 0 and k > 0. Note that the choice k², instead of -k², in Eq. (1.9) facilitates this by making ϕ either grow or decay monotonically in the x-direction instead of oscillating. The boundary condition (1.2a) is automatically satisfied if D = 0. The boundary condition (1.2b) is satisfied provided that

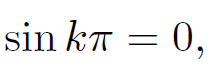 (1.12)

which implies that k is a positive integer, n (say). So, our solution reduces to

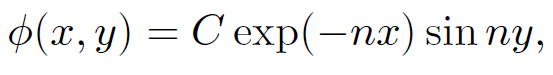 (1.13)

where B has been absorbed into C. Note that this solution is only able to satisfy the final boundary condition (1.3) provided ϕ₀(y) is proportional to sin ny. Thus, at first sight, it would appear that the method of separation of variables only works for a very special subset of boundary conditions. However, this is not the case. Now comes the clever bit! Since Poisson's equation is linear, any linear combination of solutions is also a solution. We can therefore form a more general solution than (1.13) by adding together lots of solutions involving different values of n. Thus,

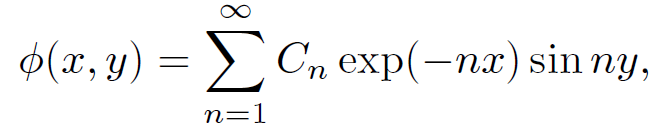 (1.14)

where the C_n are constants. This solution automatically satisfies the boundary conditions (1.2) and (1.8). The final boundary condition (1.3) reduces to

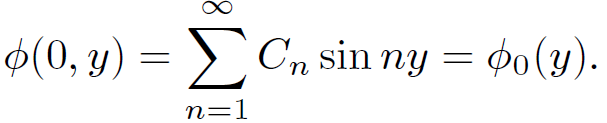 (1.15)

The question now is what choice of the C_n fits an arbitrary function ϕ₀(y)? To answer this question we can make use of two very useful properties of the functions sin ny. Namely, that they are mutually orthogonal and form a complete set. The orthogonality property of these functions manifests itself through the relation

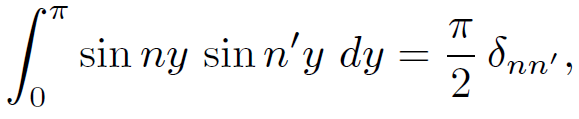 (1.16)

where the function δ_nnʹ = 1 if n = nʹ and 0 otherwise is called a Kroenecker delta. The completeness property of sine functions means that any general function ϕ₀(y) can always be adequately represented as a weighted sum of sine functions with various different n values. Multiplying both sides of Eq. (1.15) by sin nʹy and integrating over y we obtain

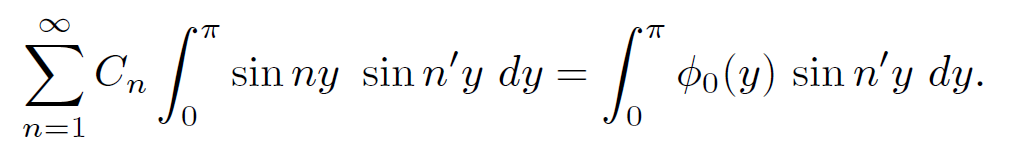 (1.17)

The orthogonality relation yields

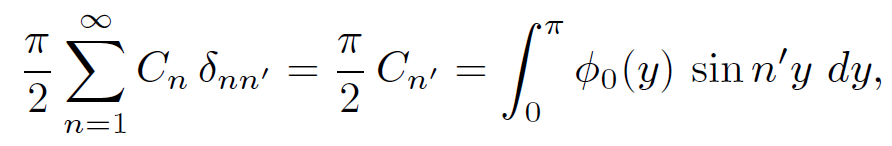 (1.18)

so

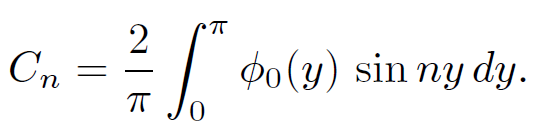 (1.19)

Thus, we now have a general solution to the problem for any driving potential ϕ₀(y). If the potential ϕ₀(y) is constant then

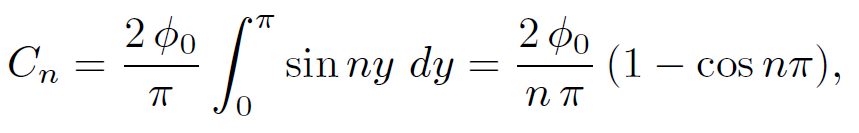 (1.20)

giving

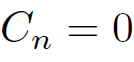 (1.21)

for even n, and

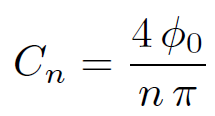 (1.22)

for odd n. Thus,

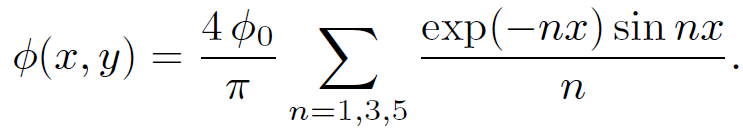 (1.23)

This potential can be summed explicitly to give

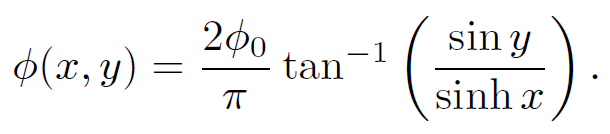 (1.24)

In this form it is easy to check that Poisson's equation is obeyed and that all of the boundary conditions are satisfied. In the above problem we write the potential as the product of one dimensional functions. Some of these functions grow and decay monotonically (i.e., the exponential functions) and the others oscillate (i.e., the sinusoidal functions). The success of the method depends crucially on the orthogonality and completeness of the oscillatory functions. A set of functions fn(x) is orthogonal if the integral of the product of two different members of the set over some range is always zero:

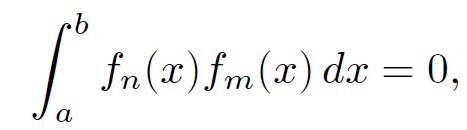 (1.25)

for n ≠ m. A set of functions is complete if any other function can be expanded as a weighted sum of them. It turns out that the scheme set out above can be generalized to more complicated geometries. For instance, in spherical geometry the monotonic functions are power law functions of the radial variable and the oscillatory functions are Legendre polynomials. The latter are both mutually orthogonal and form a complete set. There are also cylindrical, ellipsoidal, hyperbolic, toroidal, etc. coordinates. In all cases, the associated oscillating functions are mutually orthogonal and form a complete set. This implies that the method of separation of variables is of quite general applicability.