We come now to the key assertion of this chapter, the theoretically interesting and practically useful theorem that if α^∗(.) is an optimal control, then there exists a function p^∗(.), called the costate, that satisfies a certain maximization principle. We should think of the function p^∗(.) as a sort of Lagrange multiplier, which appears owing to the constraint that the optimal curve x^∗(.) must satisfy (ODE). And just as conventional Lagrange multipliers are useful for actual calculations, so also will be the costate.

We quote Francis Clarke [C2]: “The maximum principle was, in fact, the culmination of a long search in the calculus of variations for a comprehensive multiplier rule, which is the correct way to view it: p(t) is a “Lagrange multiplier” . . . It makes optimal control a design tool, whereas the calculus of variations was a way to study nature.”

1.1 FIXED TIME, FREE ENDPOINT PROBLEM. Let us review the

basic set-up for our control problem.

We are given A ⊆ R^m and also f : Rⁿ×A → Rⁿ, x⁰ ∈ Rⁿ. We as before denote the set of admissible controls by

                   A = {α(.) : [0,∞) → A | α(.) is measurable}.

Then given α(.) ∈ A, we solve for the corresponding evolution of our system:

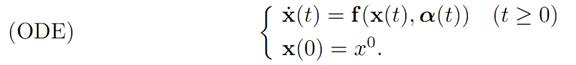
We also introduce the payoff functional

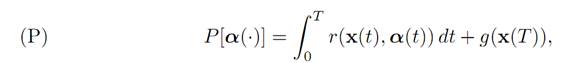
where the terminal time T > 0, running payoff r : Rⁿ ×A → R and terminal payoff

g : Rⁿ → R are given.

BASIC PROBLEM: Find a control α^∗(.) such that

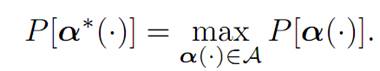
The Pontryagin Maximum Principle, stated below, asserts the existence of a function p^∗(.), which together with the optimal trajectory x^∗(.) satisfies an analog of Hamilton’s ODE from §4.1. For this, we will need an appropriate Hamiltonian:

DEFINITION. The control theory Hamiltonian is the function

                               H(x, p, a) := f (x, a) .p + r(x, a)             (x, p ∈ Rⁿ, a ∈ A).

THEOREM 1.1 (PONTRYAGIN MAXIMUM PRINCIPLE). Assume α^∗(.) is optimal for (ODE), (P) and x^∗(.) is the corresponding trajectory.

Then there exists a function p^∗ : [0, T] → Rⁿ such that

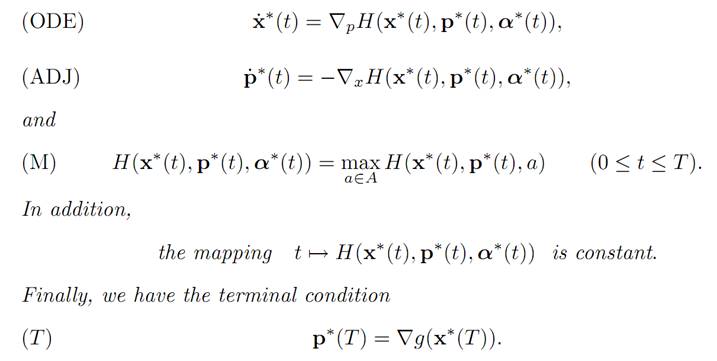
REMARKS AND INTERPRETATIONS. (i) The identities (ADJ) are the adjoint equations and (M) the maximization principle. Notice that (ODE) and  (ADJ) resemble the structure of Hamilton’s equations,

We also call (T) the transversality condition and will discuss its significance later.

(ii) More precisely, formula (ODE) says that for 1 ≤ i ≤ n, we have

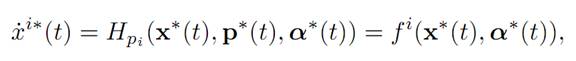
which is just the original equation of motion. Likewise, (ADJ) says

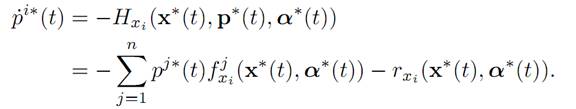
1.2 FREE TIME, FIXED ENDPOINT PROBLEM. Let us next record the appropriate form of the Maximum Principle for a fixed endpoint problem.

As before, given a control α(.) ∈ A, we solve for the corresponding evolution of our system:

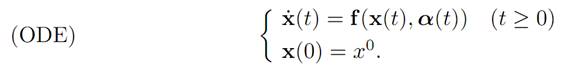
Assume now that a target point x¹ ∈ Rⁿ is given. We introduce then the payoff functional

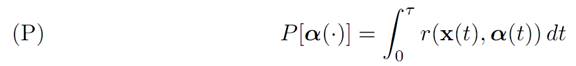
Here r : Rⁿ × A → R is the given running payoff, and τ = τ [α()] ≤ ∞ denotes the first time the solution of (ODE) hits the target point x¹.

As before, the basic problem is to find an optimal control α^∗(.) such that

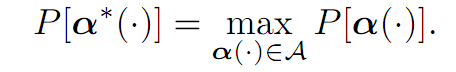
Define the Hamiltonian H .

THEOREM 1.2 (PONTRYAGIN MAXIMUM PRINCIPLE). Assume α^∗(.) is optimal for (ODE), (P) and x^∗(.) is the corresponding trajectory.

Then there exists a function p^∗ : [0, τ ^∗] → Rⁿ such that

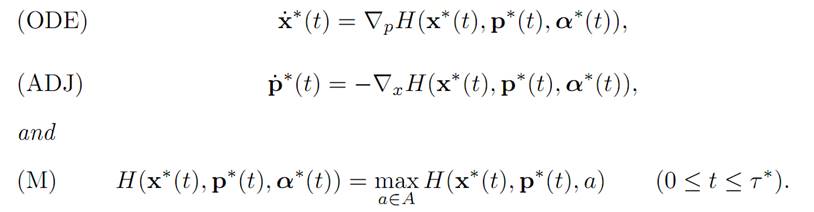
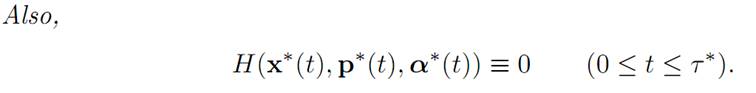
Here τ^∗ denotes the first time the trajectory x^∗(.) hits the target point x¹. We call x^∗(.) the state of the optimally controlled system and p^∗(.) the costate.

REMARK AND WARNING. More precisely, we should define

                                    H(x, p, q, a) = f (x, a) . p + r(x, a)q                               (q ∈ R).

A more careful statement of the Maximum Principle says “there exists a constant q ≥ 0 and a function p^∗ : [0, t^∗] → Rⁿ such that (ODE), (ADJ), and (M) hold”.

If q > 0, we can renormalize to get q = 1, as we have done above. If q = 0, then H does not depend on running payoff r and in this case the Pontryagin Maximum Principle is not useful. This is a so–called “abnormal problem”.

[B-CD] M. Bardi and I. Capuzzo-Dolcetta, Optimal Control and Viscosity Solutions of Hamilton-Jacobi-Bellman Equations, Birkhauser, 1997.

[B-J] N. Barron and R. Jensen, The Pontryagin maximum principle from dynamic programming and viscosity solutions to first-order partial differential equations, Transactions AMS 298 (1986), 635–641.

[C1] F. Clarke, Optimization and Nonsmooth Analysis, Wiley-Interscience, 1983.

[C2] F. Clarke, Methods of Dynamic and Nonsmooth Optimization, CBMS-NSF Regional Conference Series in Applied Mathematics, SIAM, 1989.

[Cr] B. D. Craven, Control and Optimization, Chapman & Hall, 1995.

[E] L. C. Evans, An Introduction to Stochastic Differential Equations, lecture notes avail-able at http://math.berkeley.edu/˜ evans/SDE.course.pdf.

[F-R] W. Fleming and R. Rishel, Deterministic and Stochastic Optimal Control, Springer, 1975.

[F-S] W. Fleming and M. Soner, Controlled Markov Processes and Viscosity Solutions, Springer, 1993.

[H] L. Hocking, Optimal Control: An Introduction to the Theory with Applications, OxfordUniversity Press, 1991.

[I] R. Isaacs, Differential Games: A mathematical theory with applications to warfare and pursuit, control and optimization, Wiley, 1965 (reprinted by Dover in 1999).

[K] G. Knowles, An Introduction to Applied Optimal Control, Academic Press, 1981.

[Kr] N. V. Krylov, Controlled Diffusion Processes, Springer, 1980.

[L-M] E. B. Lee and L. Markus, Foundations of Optimal Control Theory, Wiley, 1967.

[L] J. Lewin, Differential Games: Theory and methods for solving game problems with singular surfaces, Springer, 1994.

[M-S] J. Macki and A. Strauss, Introduction to Optimal Control Theory, Springer, 1982.

[O] B. K. Oksendal, Stochastic Differential Equations: An Introduction with Applications, 4th ed., Springer, 1995.

[O-W] G. Oster and E. O. Wilson, Caste and Ecology in Social Insects, Princeton UniversityPress.

[P-B-G-M] L. S. Pontryagin, V. G. Boltyanski, R. S. Gamkrelidze and E. F. Mishchenko, The Mathematical Theory of Optimal Processes, Interscience, 1962.

[T] William J. Terrell, Some fundamental control theory I: Controllability, observability,  and duality, American Math Monthly 106 (1999), 705–719.