
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
LINEAR AND NONLINEAR PHENOMENA
المؤلف:
Mark Csele
المصدر:
FUNDAMENTALS OF LIGHT SOURCES AND LASERS
الجزء والصفحة:
p219
21-3-2016
2666
LINEAR AND NONLINEAR PHENOMENA
Most effects in the physical world are linear. Basic physics shows us that effects such as the deflection of a steel ruler on a table under the influence of a weight (as in Figure 1.1) is directly proportional to the weight applied to it. If a given weight deflects the ruler 1 cm, doubling the applied weight will cause a deflection of 2 cm. The ruler is modeled as a simple spring in which the deflection is governed by the applied force according to
F = kx (1.1)
where F is the applied force, k the spring constant of the material, and x the deflection or displacement. Like most physical relationships, the deflection of the ruler is

Figure 1.1. Generation of second harmonic light.
linear with the force applied. If, however, enough force is applied to the ruler, the deflection is found to be nonlinear and is related to the force applied by a nonlinear relationship such as
F = k1x + k2x2 + k3x3 …. (1.2)
High-order terms such as x2, x3, and beyond enter into the equation, which is no longer linear. It is important to note that this nonlinear behavior occurs only when large forces are applied to the material. When forces are small (i.e., the deflection of the ruler is small compared to the length of the ruler), the relationship is quite linear and governed by equation (1.2). As force is increased, though, stresses will be induced in the material, which will cause permanent damage (in this case, a bent ruler), but before this happens, nonlinear behavior will be seen. In a nutshell, for small forces the behavior of the system is linear, for large forces it is nonlinear, and for enormous forces the system is damaged.

Figure 1.2. Linear relationship: deflection of a steel ruler.
Many optical materials behave in a similar manner; when the force applied (i.e., light intensity) is small, they are quite linear, but when a large force is applied, nonlinear behavior is exhibited. Consider the structure of a quartz crystal: a lattice with atoms placed at regular patterns. Electrons in the crystal are held to the nucleus of each atom by a force similar to a spring. When low and moderate light intensities are incident on such a crystal, electrons behave in a linear manner. Bonds stretch in response to an electric field in a linear manner.
Now that the behavior of a simple system can be defined as linear or nonlinear, we can apply the same principles to the behavior of certain materials, such as quartz, when intense laser beams travel through them and predict what happens when an electric field such as the field of an electromagnetic wave such as light interacts with atoms in a crystal. We know from an earlier chapter that the structure of the atoms in crystals consists of a nucleus with shells of electrons surrounding it (the Bohr model is sufficient to describe the atom for our purposes). The outer (valence) electrons in these atoms are more loosely bound to the nucleus than inner electrons and may even be removed (i.e., the atom ionized) when enough energy is injected into the atom.
Using the Bohr analogy, electrons are held in orbit by linear forces, and the radius of the orbit itself is governed by the same type of linear force equation that describes the deflection of the ruler in our example. When light impinges on the atom, it can cause the valence electrons to relocate in the space around the atom in step with the electric field of the incident light. Only valence electrons are affected in such an interaction because the nucleus is too heavy to be affected by an electric field, and electrons in the inner shell are bound very tightly to the nucleus. Valence electrons are held to the atom by comparatively weak forces. When an intense electric field strikes an atom, valence electrons in the shell move to one side of the atom, and the electron shell becomes eccentric and offset. Instead of a spherical shell (in which the shell is centered around the positive nucleus and hence there is no electric dipole), electrons literally move toward one end of the atom and the entire atom becomes polarized. A positive and a negative end develop on the atom, and an electric dipole with a dipole moment develops in the direction of the electric field applied.
In the presence of an applied electric field, atoms in the crystal become polarized in this manner, and the entire material becomes polarized on a localized level (around the intense beam). This is a macroscopic charge polarization of the material, and the amount of charge polarization depends on the intensity of the applied electric field according to
P =aE (1.3)
where a is the coefficient of polarizability for the material and E is the applied electric field in V/cm. This is a linear relationship, which, like the previous relationship between force and deflection [equation (1.1)] applies for small applied forces such as those encountered everyday: the intensities of light sources such as sunlight and most artificial lights. Because of this, nonlinear effects are not seen when, for example, red light passes through quartz. In the presence of a weak electric field a polarization is produced that is in step with the applied electric field. This polarization and reradiation of photons results in a slowing of the velocity of light through the crystal (this in the origin of the index of refraction of the material), but no change occurs in the nature of the light passing through the crystal.
Now, when the applied force is very large, nonlinear effects are exhibited for the same reason that the ruler exhibits nonlinear behavior. The charge polarization becomes nonlinear according to a geometric series:
P = a1E + a2E2 + a3E3…… (1.4)
The nonlinearity of the charge polarization becomes apparent, and high-order terms such as a2 and a3 contribute to the polarization. To accomplish this nonlinear polarization, an intense electric field is required. The electron is held to the positive nucleus by an internal force of about 109 V/cm. Normal light sources with electric fields below 100 V/cm exhibit only linear optical effects. Few sources exist with a high enough electric field (comparable to the internal force) to generate nonlinear effects. A focused laser beam, for example, can impress an electric field of 106 to 107 V/cm on a crystal. Even higher intensities, with even higher electric fields, can be found inside the cavities of most lasers (where the intracavity intensities are often 100 times the external intensity).
To demonstrate mathematically how second harmonic light is produced under such conditions (e.g., how the ruby laser at 694.3 nm was doubled to 347.2 nm in the example at the beginning of the chapter) consider equation (11.4), in which we substitute for the applied electric field E:
E = E0 cos ⍵t (1.5)
where ⍵ is the angular frequency of the light (2πf ). Equation (11.4) then becomes
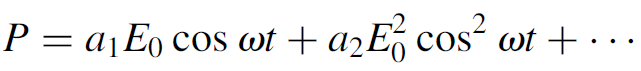 (1.6)
(1.6)
Trigonometric substitution can be made for the cos2 term as
 (1.7)
(1.7)
so that equation (1.6) becomes
 (1.8)
(1.8)
This leads to an interesting conclusion since the third term in equation (1.8) contains a term with order 2⍵; one component of the charge polarization equation is at twice the fundamental frequency of the original laser beam. As the incident beam falls on the crystal, oscillating electric dipoles absorb light at a frequency ⍵ and reradiate it at the same frequency v and at twice the original frequency 2⍵. The total energy of the beam is not altered much, but is now split between two components. This is the second harmonic of the original beam and the effect is called second-harmonic generation (SHG).
Equation (1.8) reveals not two, but three output terms: in addition to the fundamental (⍵) and second-harmonic (2⍵) term, a constant term ½ a2E20, which represents a DC offset or steady polarization. It also represents an optical rectification analogous to that of a diode rectifying an AC voltage. Indeed, this DC signal (although a minute quantity) can be detected across a nonlinear crystal by placing electrodes on either side of the crystal, and this signal is proportional to the intensity of the light beam passing through the crystal.
 الاكثر قراءة في مواضيع عامة في علم البصريات
الاكثر قراءة في مواضيع عامة في علم البصريات
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















