A magic square is a square grid in which distinct whole numbers are written into each cell of the grid in such a way that each horizontal row and each vertical column, and each diagonal add up to the same number.

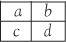
Squares with just one row and one column are technically magic squares but are very boring so we’ll forget them. There is no such thing as a magic square with two rows and two columns. If there were it would have the form shown. Since the row additions and the column additions should be equal, then a + b = a + c. This means b = c, contradicting the fact that all the entries must be distinct.

The Lo Shu square

As 2×2 squares do not exist, we’ll look at 3×3 arrays and attempt to construct one with a grid. We’ll start with a normal magic square, one where the grid is filled out with the consecutive numbers 1, 2, 3, 4, 5, 6, 7, 8 and 9.

For such a small square it is possible to construct a 3×3 magic square by the ‘trial and test’ method, but we can first make some deductions to help us along. If we add up all the numbers in the grid we have

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45

and this total would have to be the same as adding the totals of 3 rows. This shows that each row (and column and diagonal) must add up to 15. Now let’s look at the middle cell – we’ll call this c. Two diagonals involve c as does the middle row and the middle column. If we add the numbers in these four lines together we get 15 +15 +15 +15 = 60 and this must equal all the numbers added together plus 3 extra lots of c. From the equation 3c + 45 = 60, we see that c must be 5. Other facts can also be learned such as not being able to place a 1 in a corner cell. Some clues gathered, we are in a good position to use the trial and test method. Try it!

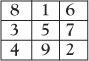
A solution for the 3×3 square by the Siamese method

Of course we’d like a totally systematic method for constructing magic squares. One was found by Simon de la Loubère, the French ambassador to the King of Siam in the late 17th century. Loubère took an interest in Chinese mathematics and wrote down a method for constructing magic squares that have an odd number of rows and columns. This method starts by placing a 1 in the middle of the first row and ‘going up and across and rotating if necessary’ to place the 2 and subsequent numbers. If blocked the next number beneath the current number is used.

Remarkably this normal magic square is essentially the only one with 3 rows and 3 columns. Every other 3×3 magic square can be obtained from this one by rotating numbers about the middle and/or reflecting numbers of the square in the middle column or middle row. It is called the ‘Lo Shu’ square and was known in China around 3000BC. Legend says that it was first seen on the back of a turtle emerging from the Lo river. The local people took this as a sign from the gods that they would not be freed of pestilence unless they increased their offerings.

If there is one 3×3 magic square, how many distinct 4×4 magic squares are there? The staggering answer is that there are 880 different ones (and be prepared, there are 2,202,441,792 magic squares of order 5). We don’t know how many squares there are for general values of n.

Dürer and Franklin’s squares

The Lo Shu magic square is well known for its age and uniqueness but one 4×4 magic square has become iconic for its association with a famous artist. It also has many more properties than some run of the mill magic squares that make up the 880 different versions. This is the 4×4 square in Albrecht Dürer’s engraving of Melancholia, which he made in the year 1514.

In Dürer’s square all the rows add up to 34, as do the columns, the diagonals, and the 2×2 small squares which make up the complete 4×4 square. Dürer even managed to ‘sign’ his masterpiece with the date of its completion in the middle of the lowest row.

The American scientist and diplomat Benjamin Franklin saw that constructing magic squares was a useful tool for sharpening the mind. He was adept at this, and to this day mathematicians have little idea how he did it; large magic squares cannot be constructed by serendipity. Franklin confessed that in his youth he had wasted much time over them despite not being taken with the ‘Arithmetick’ as a boy. Here’s one he discovered in his youth.

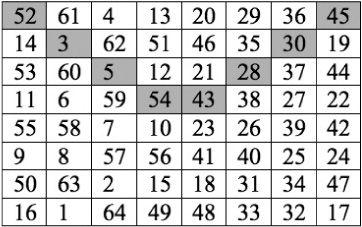
In this normal magic square there are all kinds of symmetries. All the rows, columns and diagonals add up to 260, as do the ‘bent rows’, one of which we’ve highlighted. There are many other things to discover – like the sum of the central 2×2 square plus the four corner boxes, which also adds up to 260. Look closely and you’ll find an interesting result for every 2×2 square.

Squared squares

Some magic squares can have cells occupied by different squared numbers. The problem of constructing these was posed by the French mathematician Edouard Lucas in 1876. To date no 3×3 square of squares has been found, although one has come close.

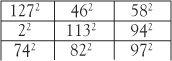
All rows and columns and one diagonal of this square add up to the magic sum 21,609 but the other diagonal fails since 127² + 113² + 97² = 38,307. If you’re tempted to find one yourself you should take note of a proven result: the centre cell value must be greater than 2.5 × 10²⁵ so there’s little point in looking for a square with small numbers! This is serious mathematics which has a connection with elliptic curves, the topic used to prove Fermat’s Last Theorem. It has been proved there are no 3×3 magic squares whose entries are cubes or fourth powers.

The search for squared squares has, however, been successful for larger squares. Magic 4×4 and 5×5 squared squares do exist. In 1770 Euler produced an example without showing his method of construction. Whole families have since been found linked to the study of the algebra of quaternions, the four-dimensional imaginary numbers.

Exotic magic squares

Large magic squares may have spectacular properties. A 32×32 array has been produced by magic square expert William Benson in which the numbers, their squares, and their cubes all form magic squares. In 2001 a 1024×1024 square was produced in which all powers of elements up to the fifth power make magic squares. There are many results like these.

We can create a whole variety of other magic squares if the requirements are relaxed. The normal magic squares are in the mainstream. Removing the condition that the sum of the diagonal elements must equal the sums of the rows, and of the columns, ushers in a plethora of specialized results. We can search for squares whose elements consist only of prime numbers, or we may consider shapes other than squares which have ‘magic properties’. By going into higher dimensions we are led to consider magic cubes and hypercubes.

But the prize for the most remarkable magic square of all, certainly for curiosity value, must go to a humble 3×3 square produced by the Dutch electronic engineer and wordsmith Lee Sallows:

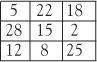
What is so remarkable about this? First write out the numbers in words:

Then count the number of letters making up each word to obtain:

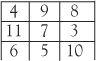
Remarkably, this is a magic square consisting of the consecutive numbers 3, 4, 5, up to 11. We also find that the number of letters of the magic sums of both 3×3 squares (21 and 45) is 9 and fittingly 3 × 3 = 9.

the condensed idea

Mathematical wizardry