Calculus is a central plank of mathematics. It would now be rare for a scientist, engineer or a quantitative economist not to have come across Calculus, so wide are its applications. Historically it is associated with Isaac Newton and Gottfried Leibniz who pioneered it in the 17th century. Their similar theories resulted in a priority dispute over who was the discoverer of Calculus. In fact, both men came to their conclusions independently and their methods were quite different.

Since then Calculus has become a huge subject. Each generation bolts on techniques they think should be learned by the younger generation, and these days textbooks run beyond a thousand pages and involve many extras. For all these add-ons, what is absolutely essential is differentiation and integration, the twin peaks of Calculus as set up by Newton and Leibniz. The words are derived from Leibniz’s differentialis (taking differences or ‘taking apart’) and integralis (the sum of parts, or ‘bringing together’).

In technical language, differentiation is concerned with measuring change and integration with measuring area, but the jewel in the crown of Calculus is the ‘star result’ that they are two sides of the same coin – differentiation and integration are the inverses of each other. Calculus is really one subject, and you need to know about both sides. No wonder that Gilbert and Sullivan’s ‘very model of a modern Major General’ in The Pirates of Penzance proudly proclaimed them both:

With many cheerful facts about the square of the hypotenuse.
I’m very good at integral and differential calculus.

Differentiation

Scientists are fond of conducting ‘thought experiments’ – Einstein especially liked them. Imagine we are standing on a bridge high above a gorge and are about to let a stone drop. What will happen? The advantage of a thought experiment is that we do not actually have to be there in person. We can also do impossible things like stopping the stone in mid-air or watching it in slow motion over a short time interval.

According to Newton’s theory of gravity, the stone will fall. Nothing surprising in that; the stone is attracted to the earth and will fall faster and faster as the hand on our stopwatch ticks on. Another advantage of a thought experiment is that we can ignore complicating factors like air resistance.

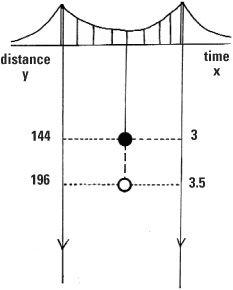
What is the stone’s speed at a given instant of time, say when the stopwatch reads exactly 3 seconds after it has been released? How can we work this out? We can certainly measure average speed but our problem is to measure instantaneous speed. As it’s a thought experiment, why don’t we stop the stone in midair and then let it move down a short distance by taking a fraction of a second more? If we divide this extra distance by the extra time we will have the average speed over the short time interval. By taking smaller and smaller time intervals the average speed will be closer and closer to the instantaneous speed at the place where we stopped the stone. This limiting process is the basic idea behind Calculus.

We might be tempted to make the small extra time equal to zero. But in our thought experiment, the stone has not moved at all. It has moved no distance and taken no time to do it! This would give us the average speed 0/0 which the Irish philosopher Bishop Berkeley famously described as the ‘ghosts of departed quantities’. This expression cannot be determined – it is actually meaningless. By taking this route we are led into a numerical quagmire.

To go further we need some symbols. The exact formula connecting the distance fallen y and the time x taken to reach there was derived by Galileo:

y = 16 × x²

The factor ‘16’ appears because feet and seconds are the chosen measurement units. If we want to know, say, how far the stone has dropped in 3 seconds we simply substitute x = 3 into the formula and calculate the answer y = 16 × 3² = 144 feet. But how can we calculate the speed of the stone at time x = 3?

Let’s take a further 0.5 of a second and see how far the stone has travelled between 3 and 3.5 seconds. In 3.5 seconds the stone has travelled y = 16 × 3.5² = 196 feet, so between 3 and 3.5 seconds it has fallen 196 − 144 = 52 feet. Since speed is distance divided by time, the average speed over this time interval is 52/0.5 = 104 feet per second. This will be close to the instantaneous speed at x = 3, but you may well say that 0.5 seconds is not a small enough measure. Repeat the argument with a smaller time gap, say 0.05 seconds, and we see that the distance fallen is 148.84 – 144 = 4.84 feet giving an average speed of 4.84/0.05 = 96.8 feet per second. This indeed will be closer to the instantaneous speed of the stone at 3 seconds (when x = 3).

We must now take the bull by the horns and address the problem of calculating the average speed of the stone between x seconds and slightly later at x + h seconds. After a little symbol shuffling we find this is

16 × (2x) + 16 × h

As we make h smaller and smaller, like we did in going from 0.5 to 0.05, we see that the first term is unaffected (because it does not involve h) and the second term itself becomes smaller and smaller. We conclude that

v = 16 × (2x)

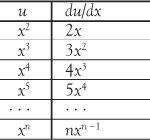
where v is the instantaneous velocity of the stone at time x. For example, the instantaneous velocity of the stone after 1 second (when x = 1) is 16 × (2 × 1) = 32 feet per second; after 3 seconds it is 16 × (2 × 3) which gives 96 feet per second.

If we compare Galileo’s distance formula y = 16 × x² with the velocity formula v = 16 × (2x) the essential difference is the change x² to 2x. This is the effect of differentiation, passing from u= x² to the derivative 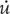= 2x. Newton called 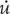= 2x a ‘fluxion’ and the variable x a fluent because he thought in terms of flowing quantities. Nowadays we frequently write u = x² and its derivative as du/dx = 2x. Originally introduced by Leibniz, this notation’s continued use represents the success of the ‘d’ism of Leibniz over the dotage of Newton’.

The falling stone was one example, but if we had other expressions that u stood for we could still calculate the derivative, which can be useful in other contexts. There is a pattern in this: the derivative is formed by multiplying by the previous power and subtracting 1 from it to make the new power.

Integration

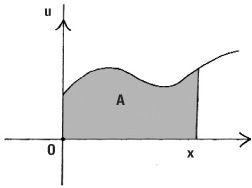
The first application of integration was to measure area. The measurement of the area under a curve is done by dividing it into approximate rectangular strips, each with width dx. By measuring the area of each and adding them up we get the ‘sum’ and so the total area. The notation S standing for sum was introduced by Leibniz in an elongated form ∫. The area of each of the rectangular strips is udx, so the area A under the curve from 0 to x is

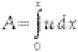
If the curve we’re looking at is u = x², the area is found by drawing narrow rectangular strips under the curve, adding them up to calculate the approximate area, and applying a limiting process to their widths to gain the exact area. This answer gives the area

A = x³/3

For different curves (and so other expressions for u) we could still calculate the integral. Like the derivative, there is a regular pattern for the integral of powers of x. The integral is formed by dividing by the ‘previous power +1’ and adding 1 to it to make the new power.

The star result

If we differentiate the integral A = x³/3 we actually get the original u = x². If we integrate the derivative du/dx = 2x we also get the original u = x². Differentiation is the inverse of integration, an observation known as the Fundamental Theorem of the Calculus and one of the most important theorems in all mathematics.

Without Calculus there would be no satellites in orbit, no economic theory and statistics would be a very different discipline. Wherever change is involved, there we find Calculus.

the condensed idea

Going to the limit