في حالات كثيرة تتغيّر القوة المؤثرة على جسم ما سريعًا مع الزمن، وتكون الكمية محل اهتمام الفيزيائي هي مصطلح المتوسط الزمني للقوة (للاختصار نسميه القوة المتوسطة). على سبيل المثال، أثناء تصادم جزيئات غاز ما بحائط أو جدار، يبذل كل جزيء قوةً على الجدار خلال فترة زمنية قصيرة جدًّا، وأي جهاز ماكروسكوبي نستخدمه لقياس القوة التي تبذلها الجزيئات على الجدار سوف يكون له زمن استجابة طويل، مقارنةً بفترة التصادم أو الزمن بين التصادمات؛ وعلى ذلك فإن الجهاز يقيس فقط معدل القوة أو المتوسط الزمني للقوة.

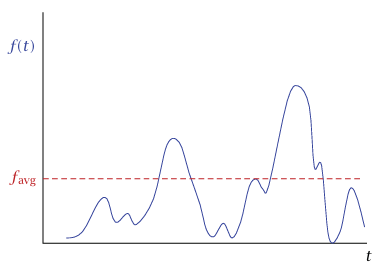
شكل 4–3: رسم بياني لقوة متغيرة تغيرًا سريعًا مع الزمن في مقابل الزمن.

افترض أن (f(t دالة ما في الزمن t. تعرف المتوسط الزمني للدالة (f(t بالمعادلة:

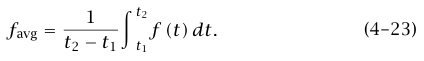
تعريف المتوسط هكذا يعتمد على t₁ وt₂، لكن f_avg في معظم الحالات التي تجذب الاهتمام لا تعتمد على ₁t وt₂ ، بشرط ألا يكون طول أخذ متوسط الفترة الزمنية صغيرًا للغاية. على سبيل المثال، شكل 4–3 عبارة عن رسم بياني للقوة المبذولة على جدار وعاء بواسطة جزيئات تتصادم مع الجدار. إذا كانت فترة أخذ المتوسط تشمل تصادمات عديدة، فإن f_avg لا تعتمد على طول فترة أخذ المتوسط. لاحظ أن تعريف f_avg يعني ضمنًا أن المساحة تحت الخط الأفقي تساوي المساحة تحت خط الرسم البياني للتراوح الفعلي للقوة مقابل الزمن.

إذا كان 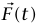 عبارة عن متجه يتغير مع الزمن، فإن متوسط  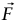الزمني يُعرف بالمثل؛ أي إن:

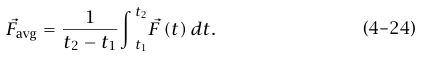
وهكذا فإن المركبة x لـ 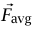 هي المتوسط الزمني للدالة (F_x(t، وبالمثل بالنسبة إلى المركبتين y وz.

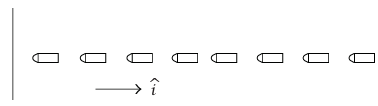
شكل 4–4: تتابع سريع للطلقات المرتطمة بالجدار عند اليسار.

نستطيع الآن حساب المتوسط الزمني للقوة التي تبذلها الجسيمات التي تصطدم بالجدار. وبدلًا من اعتبار جزيئات غاز لها توزيع سرعات استاتيكي، سوف نفترض أن الجسيمات هي طلقات مدفع رشاش؛ وبهذا تقترب جميعها من الحائط بنفس السرعة. ونُعرّف هذا النظام بأنه يتكون من جميع الطلقات التي ترتطم بالحائط أثناء فترة زمنية طولها T؛ حيث تكون T كبيرة مقارنةً بالزمن بين الطلقات. من المعادلة (4–3) نحصل على:

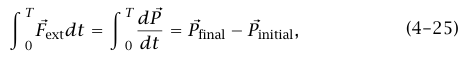
حيث 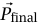 هي كمية التحرك لنظام عند زمن T و  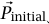هي كمية التحرك عند زمن 0.

إذا وصلت الطلقات إلى السكون في الحائط، فإن 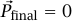. في البداية كانت جميع الطلقات تتحرك إلى اليسار بمقدار سرعة v (سرعة الطلقة هي 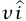–؛ حيث i متجه وحدة يشير إلى اليمين). عدد الطلقات في نظامنا الحالي هو nT؛ حيث n عدد الطلقات التي ترتطم بالحائط كل وحدة زمنية، وبناءً عليه نجد أن 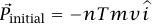؛ حيث m هي كتلة الطاقة. القوة الخارجية الوحيدة المؤثرة على نظامنا هي التي يبذلها الحائط. باستخدام المعادلة (24–4) نجد أن  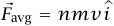هذه هي القوة المتوسطة التي يبذلها الجدار على طلقات الرصاص؛ والقوة المتوسطة التي تبذلها الطلقات على الجدار هي 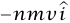. إذا كانت طلقات الرصاص، بدلا من أن تصل إلى السكون في الجدار، ترتد بعيدًا عن الجدار بسرعة 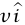، فإنه يكون لدينا 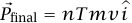، وتكون القوة المؤثرة على الجدار ضعف القوة السابقة.

المثال أدناه متقدِّم قليلًا، وقد يؤثّر في أصدقائك أو يبعدهم عنك إذا ما ناقشته في حفل ما.

مثال 4–5 (رمل في ساعة رملية). وُضعت ساعة رملية على ميزان. عندما كان كل الرمل في قاع الساعة الرملية، كانت قراءة المقياس W (أي إن وزن الساعة الرملية بالإضافة إلى الرمل كله يساوي W). كم ستكون القراءة أثناء هبوط الرمل خلال الساعة الرملية؟ للتحديد، نفترض أن كتلة ثابتة من الرمل كل وحدة زمن (نسميها ρ) تهبط خلال الساعة الرملية، وأن كل حبيبات الرمل تهبط نفس المسافة d (أي إننا نتجاهل تراكم الرمل).

هذا السؤال يمكن إجابته إما بتطبيق النظرية العامة، المعادلة (20–4)، على النظام المكون من الساعة الرملية والرمل، أو بفحص تفصيلي لما يحدث في الساعة الرملية. كلتا الطريقتين تعليميتان.

دعنا نأخذ المحور z متجهًا رأسيًّا إلى أعلى، ونأخذ 0 = z عند قاع الساعة الرملية. ارتفاع مركز كتلة النظام الساعة الرملية + الرمل) يُحدد بالمعادلة:

حيث M الكتلة الكلية للنظام، في أي لحظة من الزمن يمكن تحليل حاصل الجمع على اليمين إلى أربعة أجزاء:

(1) إسهام من الرمل في الغرفة العليا.

(2) إسهام من الرمل في الغرفة السفلى.

(3) إسهام من الرمل أثناء هبوطه.

(4) إسهام من الساعة الرملية ذاتها.

(1) يساوي t)d)m؛ حيث (m(t هي كتلة الرمل في الغرفة العليا عند زمن t. (2) يتلاشى لأن 0 = z عند القاع. (3) ثابت في الزمن لأن صورة التيار الهابط من الرمل تبدو هي نفسها في كل الأوقات. (4) ثابت في الزمن بكل وضوح. بناءً على ذلك يكون

لدينا MZ_cm = m(t)d + constant ، تفاضل كلا الطرفين بالنسبة إلى الزمن وملاحظة أن dm/dt = – ρ نحصل على pd = MdZ_cm /dt و0 = Md²Zcm /dt² لأن ρ من المفترض أن تكون ثابتة. ينتج من المعادلة (20–4) أن صافي القوة الخارجية المؤثرة على النظام يساوي صفرًا. لكن القوة الخارجية هي 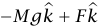 ؛ حيث 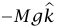 هي قوة الجاذبية التثاقلية و 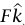هي القوة التي يبذلها الميزان؛ وبهذا نجد أن F = Mg = W؛ وقراءة الميزان تكون هي نفسها سواء أكان الرمل هابطا أم لا. (في حقيقة الأمر، هناك تأثير عابر قصير في البداية والنهاية لأن صورة الرمل الساقط متغيرة.)

بعض الناس سوف يقتنعون بأن F يجب أن تكون أقل من Mg لأن الميزان لا يشعر بوزن الرمل الذي يسقط بحرية. ومع ذلك، فهناك تأثير آخر تأثير الرمل الساقط على القاع، والذي يزيد F. التحليل السابق لمركز كتلة الحركة، الذي يتجاهل تمامًا ضرورة مناقشة هذين التأثيرين، يعني أيضًا أنهما يجب أن يتلاشيا تمامًا. يمكن أن نفهم هذا بالتفصيل. إذا كان t هو الزمن اللازم لكي تسقط حبة رمل مسافة d، فإن وزن الرمل في السقوط الحر يكون ρgt. حسابات المدفع الرشاش في المثال السابق تخبرنا أن تأثير الرمل الهابط تنشأ عنه قوة إضافية ρv تؤثّر على الميزان؛ حيث v هو مقدار سرعة حبة الرمل قبل ارتطامها بالقاع مباشرةً (وρ تشابه nm في حسابات المدفع الرشاش). بما أن v = gt، فإن القوة المؤثرة تُلاشي النقص في الوزن، كما هو متوقع. (في الحقيقة، هناك نقص وقتي عابر في قراءة المقياس قبل أن ترتطم حبة الرمل الأولى بالقاع، وزيادة وقتية أثناء هبوط الحبات الأخيرة.)

مثال 4–6 (نقل حَمَام في شاحنة) توقفت شاحنة كبيرة ذات مقطورة عند تقاطع، ولاحظ أحد المشاة أن السائق قفز خارجًا من الكابينة وضرب بغضب على جانب المقطورة مستخدمًا قطعة خشب غليظة، ثم قفز عائدًا إلى الكابينة. واستفسر الرجل الماشي فأجاب السائق صائحًا: «الحد الآمن للحمل بالنسبة إلى الإطارات هو رطل 60000. وتزن تجهيزات المقطورة 40000 رطل وهي فارغة، ولدي بالداخل 40000 رطل طيورًا حية من الحمام؛ لهذا عليَّ أن أبقي نصف وزن الحمام في الهواء.» هل ستنجح هذه الخطة؟

بفرض أن نظامنا مكون من الشاحنة بالإضافة إلى جميع المحتويات، إذا كان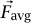 هو المتوسط الزمني للقوة المؤثرة على النظام طوال الفترة الزمنية من 0 = t إلى t = T، فإن  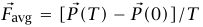حيث 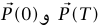 هما كمية التحرك للنظام عند هذين الزمنين. إذا افترضنا (ليس ضروريًا حقيقةً، ولكن لتبسيط المناقشة) أن هناك حدا أعلى لمقدار السرعة التي يمكن أن يطير بها الحمام، فإن مقداري  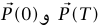يكونان محددين. وبناءً عليه، إذا جعلنا أخذ المتوسط لفترة زمنية T طويلًا بدرجة كافية، فإننا نحصل على 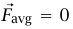. وعلى وجه الخصوص، متوسط المقدار N للقوة المتجهة لأعلى، والتي يبذلها الطريق على الإطارات يجب أن تساوي W؛ قوة الجاذبية التثاقلية المؤثرة على الشاحنة وكل محتوياتها.

كما في المثال السابق الخلاصة التي توصلنا إليها ليست مبنية على تحليل تفصيلي للقوى «الداخلية» في النظام. ومع ذلك، إذا رغب أحد في معرفة السبب في أن وزن الحمام الموجود في الهواء لم يخفّف الحمل على الإطارات، فإن الإجابة تكمن في أن رفرفة أجنحة الحمام تزيد من الضغط الذي يبذله الهواء على أرضية الشاحنة. لاحظ أن تحليلنا يفترض أن الشاحنة مغلقة بحيث تكون كل القوى المتعلقة بالديناميكا الهوائية هي قوى داخلية في نظامنا. إذا كانت المقطورة مغلقة بسياج من أسلاك قفص الطيور فقط، فإن بعض القوى الديناميكية الهوائية تنتقل إلى أجزاء مجاورة من الطريق. يجب أن يكون واضحًا أنه في هذه الحالة، إذا كانت جدران المقطورة عالية بقدر كافٍ، فإن استراتيجية السائق قد تنجح.

مثال 4–7 (علم الصواريخ). اعتبر صاروخًا في الفضاء الخارجي (حيث لا توجد جاذبية). في البداية يكون الصاروخ ساكنًا، وكتلته بالإضافة إلى كل وقوده تساوي M₀. أثناء احتراق الوقود، يندفع في اتجاه المؤخرة بمقدار سرعة ثابت u بالنسبة إلى الصاروخ يناظر ذلك تمامًا حالة امرأة مسلحة بمدفع رشاش وهي تجلس على مزلجة فوق جليد أملس، وما إن تُطلق المدفع في اتجاه المؤخرة، فإن الارتداد يُعجِّل المزلجة. ما هي سرعة الصاروخ في اللحظة التي تكون عندها كتلة الصاروخ والوقود المتبقي مساوية لـ M؟ (هذه العلاقة لا تعتمد على أي فروض بشأن معدل الاحتراق الذي لا يكون بالضرورة ثابتًا. إذا أخذت الجاذبية في الاعتبار فإن برنامج الاحتراق يكون مهما.)

لنعتبر نظامنا هو الصاروخ بالإضافة إلى كل الوقود الموجود على متنه في أي لحظة معينة. لتكن كتلة النظام هي M، وسرعة الصاروخ في هذه اللحظة هي 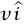؛ حيث 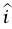 متجه وحدة يشير في اتجاه حركة الصاروخ نبحث نفس النظام (أي نفس تجمع الجسيمات) في لحظة متأخرة قليلا.

شكل 4–5 : صاروخ يطير في فضاء سحيق.

عند هذا الزمن تكون كتلة الصاروخ والوقود الموجود على متنه هي dM +M  (لاحظ أن dM كمية سالبة) وسرعة الصاروخ هي 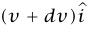. بعض جسيمات نظامنا لا تزال على متن الصاروخ؛ في الحقيقة هناك كتلة dM – من الوقود قد قُذفت من الصاروخ بسرعة  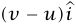بالنسبة إلى راصد قصوري. القوة المبذولة على غرفة الاحتراق بواسطة وقود الاحتراق وردود الأفعال لتلك القوى هي جميعها قوى داخلية في نظامنا؛ وبناءً على ذلك، ليس هناك قوى خارجية مؤثرة على النظام، كما أن كمية التحرك الكلية للنظام عند اللحظة الابتدائية يجب أن تساوي كمية التحرك الكلية عند لحظة متأخرة قليلًا. ومن ثُمَّ نجد أن:

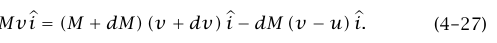
بما أن اللحظتين يمكن اعتبارهما قريبتين في الزمن كما نرغب، فإن الحد المتناهي الصغر من الرتبة الثانية dM dv يمكن إهماله مقارنةً بالحدود المتناسبة مع dM أو dv. (في الحقيقة، أهملنا بالفعل الكميات المتناهية الصغر في الحد الثاني من المعادلة أعلاه؛ لأن الجسيمات المقذوفة يمكن أن يكون لها مدى سرعات من 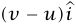 إلى 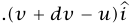 بحذف متجه الوحدة  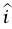نحصل على 0 = M dv + u dM. بإعادة كتابة هذه المعادلة على الصورة:

نجد أن d (ln M + v/u) = 0 وهي تعني أن ln M + v/u = constant.

إذا كانت السرعة الابتدائية (في اللحظة عندما يكون M = M₀) تساوي صفرا، فإن المقدار الثابت يأخذ القيمة In M₀، ونجد أن (u ln (M₀/M = v. إذا كانت السرعة الابتدائية v₀ نحصل على ما يسمى معادلة الصاروخ المثالية:

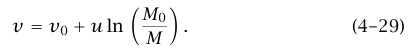
من المفيد تعليميا من وجهة نظر المهندسين، أن تُكتب هذه المعادلة على الصورة M₀/M = exp [(v – v₀)/u]. يريد المرء عادةً أن يضع كتلة معينة M₁ (تُسمى الكتلة المتفجرة) في مدار يتطلب أن يكون v – v₀ لها قيمة معينة w. في هذه الحالة يجب البدء بكتلة M₀؛ حيث M₀/M = exp (w/u). افترض وجود وقودين، الثاني قيمته أكبر مرتين من الأول؛ عندئذ إذا كان 100 = M₀/ M₁ للوقود الأول، يكون لدينا 10 = M₀/ M₁ للوقود الثاني.