Although we have finished our quantitative analyses of waves, this added chapter on the subject is intended to give some appreciation, qualitatively, for various phenomena that are associated with waves, which are too complicated to analyze in detail here. Since we have been dealing with waves for several chapters, more properly the subject might be called “some of the more complex phenomena associated with waves.”

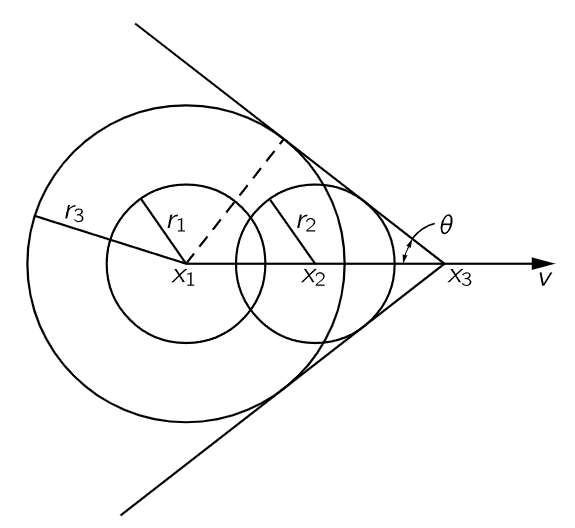
Fig. 51–1. The shock wave front lies on a cone with apex at the source and half-angle θ=sin⁻¹c_w/v.

The first topic to be discussed concerns the effects that are produced by a source of waves which is moving faster than the wave velocity, or the phase velocity. Let us first consider waves that have a definite velocity, like sound and light. If we have a source of sound which is moving faster than the speed of sound, then something like this happens: Suppose at a given moment a sound wave is generated from the source at point x₁ in Fig. 51–1; then, in the next moment, as the source moves to x₂, the wave from x₁ expands by a radius r₁ smaller than the distance that the source moves; and, of course, another wave starts from x₂. When the sound source has moved still farther, to x₃, and a wave is starting there, the wave from x₂ has now expanded to r₂, and the one from x₁ has expanded to r₃. Of course, the thing is done continuously, not in steps, and therefore, we have a series of wave circles with a common tangent line which goes through the center of the source. We see that instead of a source generating spherical waves, as it would if it were standing still, it generates a wavefront which forms a cone in three dimensions, or a pair of lines in two dimensions. The angle of the cone is very easy to figure out. In a given amount of time the source moves a distance, say x₃−x₁, proportional to v, the velocity of the source. In the meantime, the wavefront has moved out a distance r₃, proportional to c_w, the speed of the wave. Therefore, it is clear that the half-angle of opening has a sine equal to the ratio of the speed of the waves, divided by the speed of the source, and this sine has a solution only if c_w is less than v, or the speed of the object is faster than the speed of the wave:

Incidentally, although we implied that it is necessary to have a source of sound, it turns out, very interestingly, that once the object is moving faster than the speed of sound, it will make sound. That is, it is not necessary that it have a certain tone vibrational character. Any object moving through a medium faster than the speed at which the medium carries waves will generate waves on each side, automatically, just from the motion itself. This is simple in the case of sound, but it also occurs in the case of light. At first one might think nothing can move faster than the speed of light. However, light in glass has a phase velocity less than the speed of light in a vacuum, and it is possible to shoot a charged particle of very high energy through a block of glass such that the particle velocity is close to the speed of light in a vacuum, while the speed of light in the glass may be only 23 the speed of light in the vacuum. A particle moving faster than the speed of light in the medium will produce a conical wave of light with its apex at the source, like the wave wake from a boat (which is from the same effect, as a matter of fact). By measuring the cone angle, we can determine the speed of the particle. This is used technically to determine the speeds of particles as one of the methods of determining their energy in high-energy research. The direction of the light is all that needs to be measured.

This light is sometimes called Cherenkov radiation, because it was first observed by Cherenkov. How intense this light should be was analyzed theoretically by Frank and Tamm. The 1958 Nobel Prize for physics was awarded jointly to all three for this work.

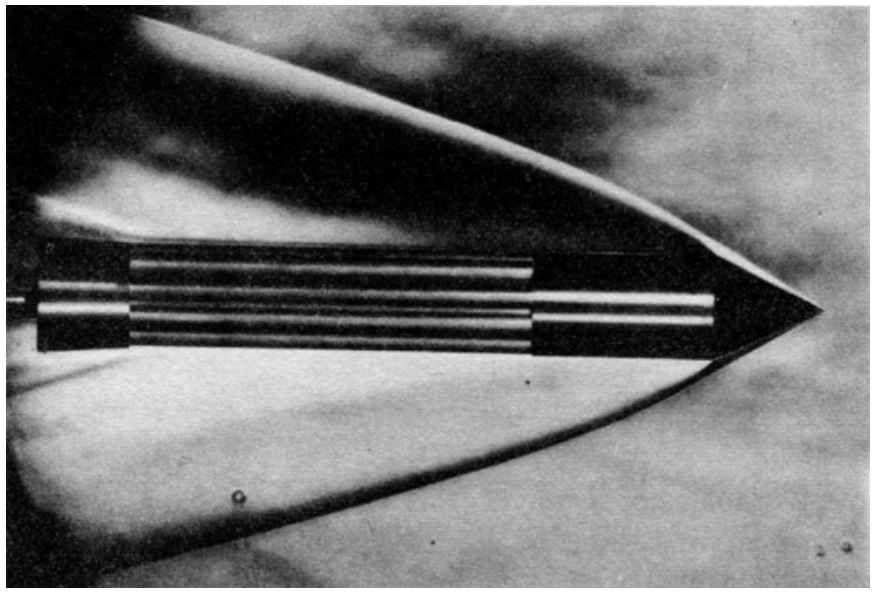
Fig. 51–2. A shock wave induced in a gas by a projectile moving faster than sound.

The corresponding circumstances in the case of sound are illustrated in Fig. 51–2, which is a photograph of an object moving through a gas at a speed greater than the speed of sound. The changes in pressure produce a change in refractive index, and with a suitable optical system the edges of the waves can be made visible. We see that the object moving faster than the speed of sound does, indeed, produce a conical wave. But closer inspection reveals that the surface is actually curved.