It's great interest to see how we can use Newton’s laws in the conservation of energy. about that energy is in fact conserved in accordance with these laws. For clarity we shall start with the simplest possible example, and then develop harder and harder examples.

The simplest example of the conservation of energy is a vertically falling object, one that moves only in a vertical direction. An object which changes its height under the influence of gravity alone has a kinetic energy T (or K.E.) due to its motion during the fall, and a potential energy mgh, abbreviated U (or P.E.), whose sum is constant:

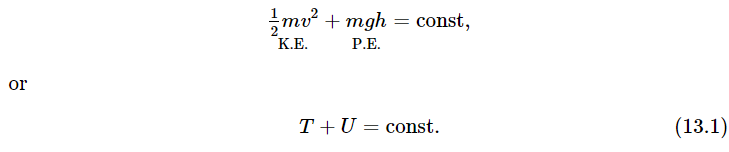
Now we would like to show that this statement is true. What do we mean, show it is true? From Newton’s Second Law we can easily tell how the object moves, and it is easy to find out how the velocity varies with time, namely, that it increases proportionally with the time, and that the height varies as the square of the time. So, if we measure the height from a zero point where the object is stationary, it is no miracle that the height turns out to be equal to the square of the velocity times a number of constants. However, let us look at it a little more closely.

Let us find out directly from Newton’s Second Law how the kinetic energy should change, by taking the derivative of the kinetic energy with respect to time and then using Newton’s laws. When we differentiate 1/2 mv² with respect to time, we obtain

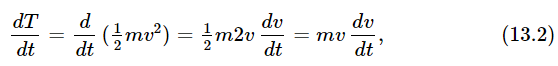
since m is assumed constant. But from Newton’s Second Law, m(dv/dt) = F, so that

In general, it will come out to be F⋅v, but in our one-dimensional case let us leave it as the force times the velocity.

Now in our simple example the force is constant, equal to −mg, a vertical force (the minus sign means that it acts downward), and the velocity, of course, is the rate of change of the vertical position, or height h, with time. Thus, the rate of change of the kinetic energy is −mg(dh/dt), which quantity, miracle of miracles, is minus the rate of change of something else! It is minus the time rate of change of mgh! Therefore, as time goes on, the changes in kinetic energy and in the quantity mgh are equal and opposite, so that the sum of the two quantities remains constant. Q.E.D.

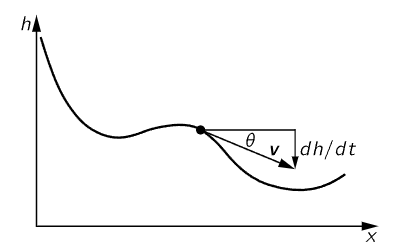
Fig. 13–1. An object moving on a frictionless curve under the influence of gravity.

We have shown, from Newton’s second law of motion, that energy is conserved for constant forces when we add the potential energy mgh to the kinetic energy 1/2 mv². Now let us look into this further and see whether it can be generalized, and thus advance our understanding. Does it work only for a freely falling body, or is it more general? We expect from our discussion of the conservation of energy that it would work for an object moving from one point to another in some kind of frictionless curve, under the influence of gravity (Fig. 13–1). If the object reaches a certain height h from the original height H, then the same formula should again be right, even though the velocity is now in some direction other than the vertical. We would like to understand why the law is still correct. Let us follow the same analysis, finding the time rate of change of the kinetic energy. This will again be mv(dv/dt), but m(dv/dt) is the rate of change of the magnitude of the momentum, i.e., the force in the direction of motion—the tangential force Ft. Thus

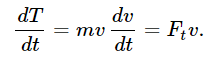
Now the speed is the rate of change of distance along the curve, ds/dt, and the tangential force F_t is not −mg but is weaker by the ratio of the vertical distance dh to the distance ds along the path. In other words,

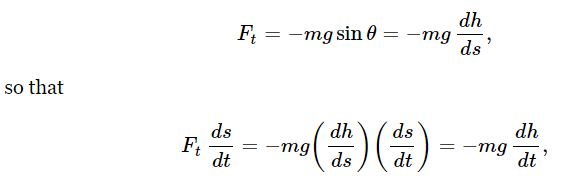
since the ds’s cancel. Thus, we get −mg(dh/dt), which is equal to the rate of change of −mgh, as before.

In order to understand exactly how the conservation of energy works in general in mechanics, we shall now discuss a number of concepts which will help us to analyze it.

First, we discuss the rate of change of kinetic energy in general in three dimensions. The kinetic energy in three dimensions is

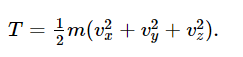
When we differentiate this with respect to time, we get three terrifying terms:

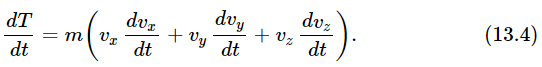
But m (dv_x/dt) is the force F_x acting on the object in the x-direction. Thus, the right side of Eq. (13.4) is F_xv_x+F_yv_y+F_zv_z. We recall our vector analysis and recognize this as F⋅v; therefore

This result can be derived more quickly as follows: if a and b are two vectors, both of which may depend upon the time, the derivative of a⋅b is, in general,

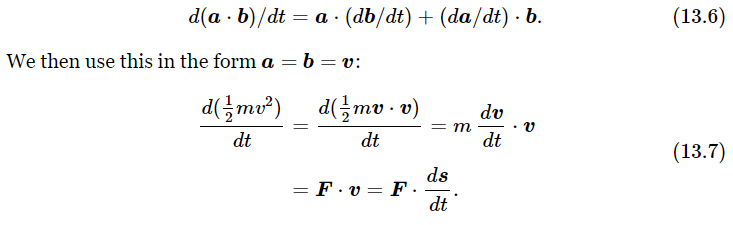
Because the concepts of kinetic energy, and energy in general, are so important, various names have been given to the important terms in equations such as these. 1/2 mv² is, as we know, called kinetic energy. F⋅v is called power: the force acting on an object times the velocity of the object (vector “dot” product) is the power being delivered to the object by that force. We thus have a marvelous theorem: the rate of change of kinetic energy of an object is equal to the power expended by the forces acting on it.

However, to study the conservation of energy, we want to analyze this still more closely. Let us evaluate the change in kinetic energy in a very short time dt. If we multiply both sides of Eq. (13.7) by dt, we find that the differential change in the kinetic energy is the force “dot” the differential distance moved:

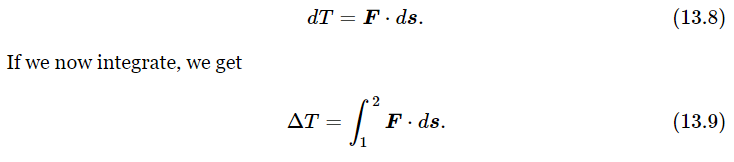
What does this mean? It means that if an object is moving in any way under the influence of a force, moving in some kind of curved path, then the change in K.E. when it goes from one point to another along the curve is equal to the integral of the component of the force along the curve times the differential displacement ds, the integral being carried out from one point to the other. This integral also has a name; it is called the work done by the force on the object. We see immediately that power equals work done per second. We also see that it is only a component of force in the direction of motion that contributes to the work done. In our simple example the forces were only vertical, and had only a single component, say F_z, equal to −mg. No matter how the object moves in those circumstances, falling in a parabola for example, F⋅s, which can be written as F_xd_x+F_yd_y+F_zd_z, has nothing left of it but F_zd_z=−mgdz, because the other components of force are zero. Therefore, in our simple case,

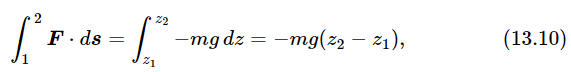
so again, we find that it is only the vertical height from which the object falls that counts toward the potential energy.

A word about units. Since forces are measured in newtons, and we multiply by a distance in order to obtain work, work is measured in newton⋅

meters (N⋅m), but people do not like to say newton-meters, they prefer to say joules (J). A newton-meter is called a joule; work is measured in joules. Power, then, is joules per second, and that is also called a watt (W). If we multiply watts by time, the result is the work done. The work done by the electrical company in our houses, technically, is equal to the watts times the time. That is where we get things like kilowatt hours, 1000 watts times 3600 seconds, or 3.6×10⁶ joules.

Now we take another example of the law of conservation of energy. Consider an object which initially has kinetic energy and is moving very fast, and which slides against the floor with friction. It stops. At the start the kinetic energy is not zero, but at the end it is zero; there is work done by the forces, because whenever there is friction there is always a component of force in a direction opposite to that of the motion, and so energy is steadily lost. But now let us take a mass on the end of a pivot swinging in a vertical plane in a gravitational field with no friction. What happens here is different, because when the mass is going up the force is downward, and when it is coming down, the force is also downward. Thus F⋅ds have one sign going up and another sign coming down. At each corresponding point of the downward and upward paths the values of F⋅ds are exactly equal in size but of opposite sign, so the net result of the integral will be zero for this case. Thus, the kinetic energy with which the mass comes back to the bottom is the same as it had when it left; that is the principle of the conservation of energy. (Note that when there are friction forces the conservation of energy seems at first sight to be invalid. We have to find another form of energy. It turns out, in fact, that heat is generated in an object when it rubs another with friction, but at the moment we supposedly do not know that.)