ما دام أينشتاين لم يعتبر الضوء بمثابة تيار من الجسيمات ينجذب – شأن أي نوع آخر من الجسيمات - بفعل قوة الجاذبية، فما الصورة الفيزيائية التي طورها بغرض اختبار وفهم ما يحدث على أرض الواقع؟

سنعود إلى تجربة إسقاط المطرقة والريشة في ضوء أن كلا منهما تملك كتلة مختلفة عن الأخرى، رأينا أن الجاذبية يتعين عليها أن تجذبهما بقوة متباينة كي تجعلهما تتسارعان نحو الأرض بالطريقة عينها تمامًا. وقد أثار هذا تساؤلاً مفاده: كيف تعرف الجاذبية مقدار الشدة الذي يجب أن تجذب به كلا منهما بحيث يسلك الاثنان السلوك

عينه؟ وعلى أي حال لماذا تريد قوة الجاذبية أساسًا منهما أن يسلكا على هذا النحو؟ الأمر عينه يحدث حين يخرج رائد الفضاء من مركبته إن المركبة تدور حول الأرض حين تكون محركاتها مطفأة؛ أي إنها في حالة سقوط حر. وحين يخرج رائد الفضاء منها ويطفو إلى جوارها في الفضاء فهو أيضًا يدور حول الأرض، في نفس مدار المركبة حول الأرض تقريبًا. ومجددًا، تتسبب الجاذبية الصادرة عن الأرض في السلوك نفسه لجسمين مختلفين تمامًا. فبدلا من التحرك في خط مستقيم بسرعة ثابتة فإن قوة الجاذبية تجتذب رائد الفضاء الذي يطفو في الفضاء والمركبة الفضائية بالطريقة نفسها تقريبا بحيث تجبر الاثنين على التحرك في مسار منحن؛ المسار المنحني ذاته.

كانت استجابة أينشتاين لهذه المعضلة هي اقتراح أنه في وجود جسم جاذب، فإن الحركة «الطبيعية» لأي جسم حوله «ليست» البقاء في سكون أو الحركة بسرعة ثابتة في خط مستقيم، وإنما اقترح أينشتاين أنه قرب الأجسام الجاذبة ككوكب الأرض يكون الفضاء نفسه مشوهًا. فهو منحن بطريقة تجعل المسار الطبيعي للأجسام التي تدور حول الجسم يكون ذلك المسار الذي نرصده: أي المدار الذي يتبعه رائد الفضاء وهو خارج المركبة والمركبة حول الأرض.

يمكن تصور الموقف وكأننا في حلبة دائرية ذات سطح مائل لسباق سيارات. في مثل هذا النوع من الحلبات يمكن لسيارتين مختلفتين للغاية أن تدورا حول الحلبة دون الحاجة سوى لتوجيه قليل للغاية من السائقين؛ وذلك لأن السيارتين مدفوعتان للسير في المسار المنحني؛ بسبب ميل مستوى سطح الحلبة عند الأطراف. إن سطح الحلبة مشوه أو منحن بحيث لم يعد من «الطبيعي» للسيارة أن تواصل السير في خط مستقيم. أيضًا لم تعد السيارة بحاجة إلى قوة موجهة كي تغير اتجاه حركتها إن «التوجيه» يوفره سطح الحلبة المهيأ على هذا النحو.

ما يقوله أينشتاين إذن هو أننا لسنا بحاجة للاستعانة بقوة - قوة الجاذبية - لإبقاء رائد الفضاء والمركبة في مدارهما حول الأرض. ليست هناك قوة بحاجة للضبط الدقيق بحيث تبقي الأجسام ذات الكتل المختلفة على المسار ذاته. بدلا من ذلك، يتبع كلُّ من رائد الفضاء والمركبة المسار الطبيعي الذي ستتبعه «كل» الأجسام لو أنها بدأت من الموضع ذاته وبالسرعة ذاتها؛ وبذا استعاض أينشتاين بالكامل عن فكرة قوى الجاذبية تماما بمفهوم جديد هو مفهوم «الفضاء المنحني».

كان الأمر غاية في البساطة. لكن بالطبع بشرط أن يستطيع المرء الإلمام في عقله بفكرة الفضاء المنحني! وهذا ليس بالأمر السهل، خاصة وأننا اعتدنا التفكير في الفضاء بوصفه مرادفا لـ «العدم». كيف يكون العدم منحنيا؟

الجواب في نظر الفيزيائيين هو أن الفضاء ليس كالعدم بل ينظر للفضاء بوصفه متصلا سلسًا منتظمًا، يمكن تشبيهه بطبقة رقيقة للغاية من الجيلي. وعندما نضع في اعتبارنا لاحقًا علم كونيات الانفجار العظيم، سنجد أن جميع العناقيد المجرية تتحرك مبتعدة بعضها عن بعض. ليس هذا راجعًا إلى أنها تتمدد فيما كان في السابق فضاءً شاغرًا أو- عدما خاويًا - وإنما الحقيقة هي أن الفضاء نفسه هو الذي يتمدد، وبالتبعية يحمل معه المجرات في مدٍّ من الفضاء المتحرك. ومرة أخرى، عند التعرض لدراسة فيزياء الكم، نكتشف أن الفيزيائيين يرون أن الفضاء مكتظ بجسيمات أساسية «افتراضية»، بعضها يظهر إلى الوجود من وقت لآخر. هذا أحد التأثيرات. ويتمثل تأثير آخر في أن الشحنة الكهربية التي يحملها الإلكترون مثلًا تتنافر مع شحنات الإلكترونات الافتراضية التي يتألف منها الفراغ الملاصق لها، وهو ما يتسبب في دفع هذه الجسيمات الافتراضية بعيدًا.

بالتفكير من هذا المنطلق - من منطلق أن الفضاء مادة من نوع ما وليس عدما - سيكون من المقبول أكثر أن نصور هذه المادة وقد تعرضت للتشويه والانحناء بصورة ما؛ بحيث لا يصير المسار الطبيعي بالضرورة خطّا مستقيما. ويُتوقع أن يؤثر هذا الانحناء، أو التقوس، على أي شيء يمر بجوار تلك المنطقة من الفضاء، بما في ذلك الضوء.

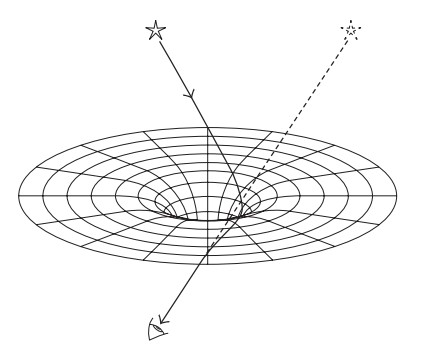
شكل 2-7: تمثيل للطريقة التي يمكن أن ينحني بها الضوء القادم من نجم بعيد بفعل انحناء الفضاء الذي تسببه الشمس.

ليست فكرة الفضاء المنحني جديدة في حد ذاتها، وفكرة الفضاء المنحني الثنائي الأبعاد مألوفة لنا جميعًا. قد يتكون الفضاء الثنائي الأبعاد من صفحة مستوية. وعلى سطح كهذا، يتحدد محيط أي دائرة C من خلال التعبير الرياضي الشهير:

C = 2πr

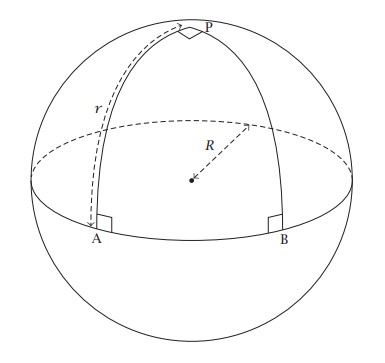
شكل 2-8: الهندسة على السطح الكروي تختلف عنها على سطح مستو.

حيث r نصف قطر الدائرة ثَمَّة نتيجة أخرى للفضاء الثنائي الأبعاد وهي أن مجموع الزوايا الداخلية للمثلث تساوي 180 درجة. لكننا قد نواجه بموقف يتخذ فيه السطح شكل الكرة. بعبارة أخرى يكون الفضاء الثنائي الأبعاد منحنيًا. في الشكل 2-8، نرى أن الدائرة التي يشكلها خط الاستواء يقع مركز سطحها عند القطب الشمالي P (وليس مركز الكرة؛ لأننا مجبرون على الالتزام بالسطح الثنائي الأبعاد). على هذا السطح، أقصر طريق بين نقطتين هو الخط المستقيم (أي الشكل الذي سيتخذه شريط مطاطي لو أنه مد بين نقطتين)؛ ومن ثَم تكون الخطوط المستقيمة بالنسبة للكرة بمثابة خطوط أقواس لدوائر كبيرة. وبذا، يكون الخط PA هو نصف القطر r الخاص بالدائرة الاستوائية داخل السطح الثنائي الأبعاد وليس نصف القطر R الممتد من مركز الكرة). إن خط الاستواء يمثل دائرة كاملة ممتدة حول الكرة، بينما نصف القطر ما هو إلا ربع دائرة كاملة حول الكرة؛ ومن ثَم على مثل هذا السطح تكون العلاقة الرياضية لهذه الدائرة بعينها كما يلي:

C = 4r

2πrوهكذا نرى أن محيط الدائرة يكون أقل من

ليست الدوائر وحدها التي تتأثر بالهندسة المنحنية، بل المثلثات أيضًا. فالمثلث PAB يتألف من ثلاثة خطوط مستقيمة متقاطعة، وزواياه الداخلية الثلاث زوايا قائمة؛ أي إن مجموعها 270 درجة، وليس 180 درجة كالمعتاد.

إن سطح الكرة ما هو إلا نوع واحد من أنواع الفضاء المنحني الثنائي الأبعاد. يبين الشكل 2-9 نوعًا آخر على شكل سرج جواد. وهنا نجد أن مجموع الزوايا الداخلية للمثلث يقل عن 180 درجة، ومحيط الدائرة أكبر من

  2πr

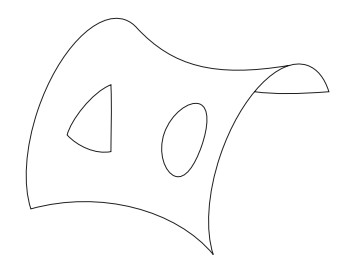
شكل 2-9 السرج شكل آخر تكون الهندسة داخل سطحه مختلفة عن الهندسة على سطح مستو.

لاحظ أن الدائرتين والمثلثين المرسومة على السطحين المقوسين، كانت أحجامها متشابهة نسبة إلى الحجم الكلي للكرة أو السرج. ولو أننا حصرنا انتباهنا في الدوائر والمثلثات الصغيرة للغاية، كنا لنحصل على نتائج مختلفة بدرجة كبيرة. فعلى المستويات الصغيرة للغاية حتى الأسطح المنحنية تميل إلى أن تكون مستوية، وفي هذه الحالة تصح الهندسة الطبيعية الخاصة بالأسطح المستوية ولو على نحو تقريبي، وهذا التقريب يتحسن كلما كان النطاق أصغر. ما نعلمه إذن من هذه الدراسة الموجزة للفضاء المنحني الثنائي الأبعاد، هو أننا نحصل على نتائج تختلف عن النتائج التي تقدمها لنا الهندسة الإقليدية المستوية المعتادة.

رغم أننا كلما درسنا الأشكال على مستوى أصغر، صارت أقرب إلى حالة الهندسة المستوية. وسنستعين بهذه النتائج عند تدبرنا لما يعنيه وجود فضاء منحن «ثلاثي الأبعاد. في البداية، من المستحيل أن نتصور ذهنيًّا شكل الفضاء المنحني الثلاثي الأبعاد. في حالة الفضاء الثنائي الأبعاد كان الأمر يسيرًا؛ لأن لدينا بُعدًا ثالثًا نستطيع تصور التقوس أو الانحناء وهو يحدث فيه. لكن أين البعد المكاني الرابع الذي سيحتوي «انحناء» الأبعاد الثلاثة؟

في الواقع، يمكن للتصور الذهني أن يكون مضللا. ألقِ نظرة على السطح المبين في الشكل 2-10. هل هو منحن؟ من الواضح أنه كذلك، من جانب ما؛ فهو شكل أسطواني. لكن يمكن أن تكون المظاهر خداعة؛ فالهندسة التي تتم على ذلك السطح هي ذاتها هندسة السطح المستوي. فعلى أي حال، يمكن عمل أسطوانة عن طريق ثني صفحة من الورق (بطريقة يستحيل بها أن تثني صفحة من الورق كي تكون كرة أو سرجًا). وإذا رسمت دائرة أو مثلثًا على صفحة مستوية من الورق ثم ثنيتها كي تكون أسطوانة، فإن خصائص تلك الأشكال ستظل ذاتها كما كانت من قبل.

لذا انسَ أمر تصور الانحناء ذهنيًّا. بدلا من ذلك نحن نعرف الفضاء بوصفه منحنيا ما دامت الهندسة «داخل» ذلك الفضاء تختلف عن الهندسة الإقليدية. فعلى أي حال، لن يحتاج الذباب الذي يزحف على سطح الكرة أو السرج أن ينظر إلى ذلك السطح من عل كي يستنتج أنه سطح منحن. فبمقدوره التوصل إلى ذلك الاستنتاج ببساطة من خلال إجراء بعض القياسات على المثلثات والدوائر داخل السطح نفسه. وهذه هي الكيفية التي سنستكشف بها هندسة الفضاء الثلاثي الأبعاد؛ ليس بواسطة وضع أنفسنا في موضع خارج الفضاء الثلاثي الأبعاد بشكل ما من أجل الحصول على نظرة كلية له، وإنما بواسطة إجراء بعض القياسات داخل الفضاء نفسه.

تعرف بالفعل — من تجارب انحناء الضوء ومن دوران المركبة ورائد الفضاء خارجها حول الأرض — أن الفضاء ينحني بالمقدار الذي تؤثر به الأرض والشمس والمجرة. فهذه الأجرام أشبه بغمازات منتشرة على امتداد السطح العريض الذي يؤلف الفضاء بأكمله. لكن إجمالا، هل هذه الغمازات موجودة على سطح مستو أم كروي أم على شكل سرج أم ماذا تحديدًا؟

رأينا من قبل كيف أن وجود جسم جاذب يؤثر على الزمن (الانزياح الأحمر الجذبوي)، والآن نرى أنه يؤثر أيضًا على المكان. ومع الوضع في الاعتبار كيف أن النسبية الخاصة قادتنا إلى استنتاج أن المكان والزمان يؤلفان زمكانًا رباعي الأبعاد،

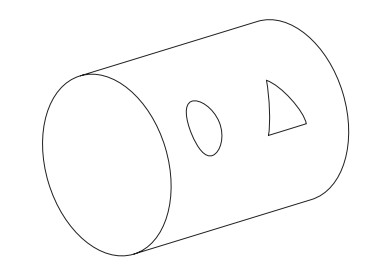
شكل 10-2: رغم حقيقة أن سطح الأسطوانة يبدو «منحنيا»، فإن هندسته ذاتها هندسة الأسطح المستوية.

قادتنا إلى استنتاج أن المكان والزمان يؤلفان زمكانًا رباعي الأبعاد، نخلص من هذا الآن إلى أنه لا يجدر بنا فقط التفكير في فضاء منحن، بل في زمكان منحن». فمحور الزمن إضافة إلى المحاور المكانية الثلاثة الأخرى تتأثر كلها بوجود جسم جاذب.

تحدثنا سابقا عن أن الأجسام تتبع مسارات طبيعية عبر الزمكان المنحني. والاسم الفعلي الذي يطلق على هذه المسارات هو «الخطوط الجيوديسية». والخط الجيوديسي هو المسار الذي يتبعه الجسم في حالة السقوط الحر، ونقصد الجسم الذي لا يخضع لأي قوى غير جذبوية، مثل التأثيرات الكهربية والمغناطيسية التأثيرات الجذبوية موضوعة بالفعل في الحسبان من خلال انحناء (الزمكان. وبعبارة أخرى في النسبية العامة، يحل الخط الجيوديسي محل الخط المستقيم في الهندسة الإقليدية المعتادة أو في النسبية الخاصة، وبذا، حين ينحني الضوء القادم من أحد النجوم قرب الشمس، فهو بهذا يتبع خطًا جيوديسيا. ما السمة المحددة للخط الجيوديسي؟ في الفضاء الإقليدي الثلاثي الأبعاد، يُعرَّف الخط المستقيم القياسي بأنه أقصر مسار بين نقطتين. أما في الزمكان، فالخط الجيوديسي يُعرف بأنه ذلك المسار بين حدثين يتسمان بأن لهما الزمن الحقيقي الأقصى. ويُعرف الزمن الحقيقي بأنه الزمن المسجل على ساعة مصاحبة للجسم إبان حركته بين النقطتين.

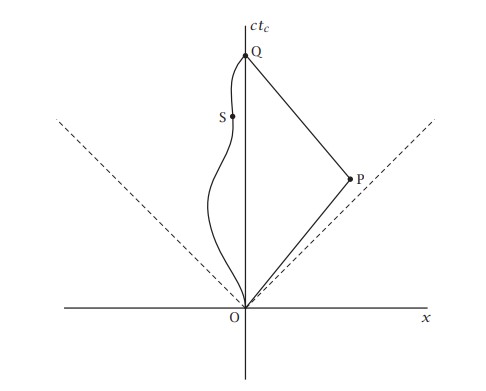
شكل 2-11: الخطوط العالمية الخاصة للتوأمين المشارك فيما يطلق عليه «معضلة التوأمين».

وهذا الشكل يبين الموقف من منظور مسؤول المراقبة. النقطة 0 تميز مغادرة رائد الفضاء لكوكب الأرض، ثم يسافر إلى الكوكب البعيد وصولا إلى النقطة P، ثم يستدير ويعود إلى الأرض، ويصل إلى النقطة Q. في الآن ذاته يظل مسؤول المراقبة ساكنا ويرسم الخط العالمي OQ. لقد أثبتنا بالفعل أنه بحلول وقت التقاء مسؤول المراقبة برائد الفضاء ستكون ساعة مسؤول المراقبة قد سجلت زمنًا أكثر من ساعة رائد الفضاء. بعبارة أخرى: سيكون زمنه الحقيقي أكبر من زمن رائد الفضاء الحقيقي. وهذا سيصح على وجه العموم. فبغض النظر عن الخط العالمي الذي سيرسمه رائد الفضاء بين النقطتين O وQ - على غرار المسار الاعتباطي المبين وهو يعبر النقطةS  مثلا - ستكون القراءة التي تسجلها ساعته دائما أقل من القراءة التي تسجلها ساعة مسؤول المراقبة. وسيكون رائد الفضاء قد تبع خطا عالميًّا يتسم بزمن حقيقي أقل من الزمن الخاص بمسؤول المراقبة. ما الأمر المميز بشأن الخط العالمي لمسؤول المراقبة بحيث يجعله يملك الزمن الحقيقي الأقصى؟ الإجابة هي أنه هو من ظل طيلة الوقت داخل إطار مرجعي قصوري، وأنه يتبع مسار سقوط حر إنه يتبع الخط الجيوديسي بين الحدثين O وQ.

بالمناسبة، لا تدع مسمى «الزمن الحقيقي» يضللك؛ فهو لا يعني بصورة ما أن هذا هو الزمن الفعلي، الصحيح، وأن غيره من الأزمنة ليس صحيحًا! أكرر هنا ما قلته من قبل عندما شرعت في تقديم الأفكار النسبية عن الأطوال والأزمنة: إن كل تقديرات المسافة والزمن مرتبطة بمنظور راصد بعينه؛ فما من وجود لمسافة أو فترة زمنية موضوعية ومستقلة عن منظور أي راصد؛ ولا وجود لما يمكن تسميته المسافة أو الزمن «المتفق عليه».

نقطة أخرى تستحق الذكر؛ أنه هي رغم أننا قدمنا فكرة الخطوط الجيوديسية في سياق مناقشتنا لتأثيرات الجاذبية، فإنها تنطبق على نحو عام وشامل؛ حتى على الحالات التي لا تشتمل على الجاذبية. ليس الأمر أننا نستخدم «الزمن الحقيقي الأقصى» في حالة، و«أقصر مسافة بين نقطتين» في حالة أخرى. ففي غياب الجاذبية، فإن الخطوط الجيوديسية التي تتسم بأن لها الزمن الحقيقي الأقصى يتفق أنها تتسم أيضًا بكونها أقصر مسافات مكانية.

إن أساس النسبية العامة هو أن المادة تُملي على الفضاء كيف ينحني، والفضاء يُملي على المادة كيف تتحرك. فالفضاء لم يعد يُنظر إليه بوصفه خشبة مسرح يؤدي عليها الممثلون - المادة والأجسام والضوء - أدوارهم، بل صار للفضاء نفسه دور يلعبه. قد تخال أنه لا بأس بكل هذا، وأن فكرة قوى الجاذبية قد حلت محلها فكرة الفضاء أو الزمكان المنحني. لكن أليس هذا محض تفضيل شخصي بشأن الكيفية التي يختار بها المرء أن يرى الأمور؟ ألا يستطيع المرء التمسك بفكرة نيوتن عن قوى الجاذبية لو أنه رغب في ذلك؟

في أغلب المواقف اليومية، تنطبق نظرية نيوتن حتى مستوى ملائم للغاية من الدقة. وحتى عند حساب مدارات الأقمار الصناعية من المواتي استخدام قانون التربيع العكسي للجاذبية. فمن الناحية الرياضية نظرية نيوتن أسهل كثيرًا في تناولها من النسبية العامة؛ ولهذا السبب وحده سيستمر الفيزيائيون في الحديث عن قوى الجاذبية وسيستخدمون ذلك، قانون نيوتن. ومع هم يدركون أن النسبية العامة تقدم تنبؤات أدق وأنها سبيل أرقى لفهم الفيزياء. فرغم أن قانون نيوتن يعد «وصفة» مفيدة لحل أغلب المشكلات – تلك التي تتضمن الجاذبية الضعيفة والسرعات الأقل بكثير عن سرعة الضوء – فإنه لا يقدم أفكارا كثيرة عما يحدث بالفعل.

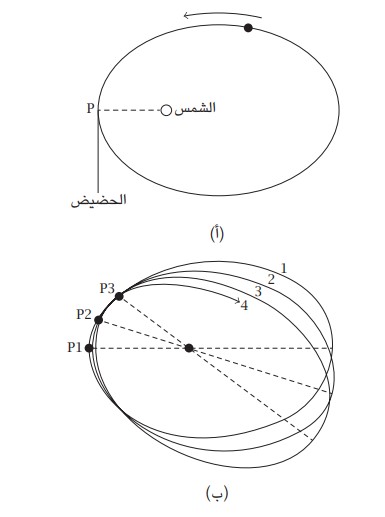
شكل 2-12: وفق ميكانيكا نيوتن، ينبغي أن يكون مدار كوكب مثل عطارد مدارا بيضاويٍّا. وفي غياب أي جسم آخر جاذب (كواكب أخرى)، من المفترض أن يظل الحضيض ثابتًا (أ). لكن وفق النظرية النسبية العامة، يجب أن يتبادر الحضيض (ب)

أفكارا كثيرة عما يحدث بالفعل. ليست النسبية العامة مجرد تفسير هندسي اختياري للجاذبية، وقد لمسنا جانبًا من هذا بالفعل حين أوضحنا أن نظرية نيوتن تنبأت بانحناء ضوء النجوم قرب الشمس — وذلك على افتراض أن الضوء مؤلف من جسيمات — حيث أنها تنبأت بمقدار خاطئ، أما النسبية العامة فتنبأت بمقدار الانحناء الصحيح.

أُجري اختبار شهير آخر للنسبية العامة في عام 1915 ، وتضمن كوكب عطارد؛ أقرب الكواكب إلى الشمس ومن ثَم أكثرها تعرضًا للجاذبية الشمسية في أقوى صورها. شأن غيره من الكواكب، يدور عطارد حول الشمس في مدار بيضاوي بحيث تمثل الشمس أحد مركزي المدار البيضاوي، كما يوضح الشكل 2-12(أ) تسمى النقطة التي يكون الكوكب فيها أقرب ما يكون إلى الشمس باسم «الحضيض». في المعتاد، ووفق ميكانيكا نيوتن من المفترض أن يظل اتجاه المدار ثابتا دون تغير، بحيث يظل الحضيض الشمسي في موضعه. لكن في الواقع، كان معروفًا أن الحضيض الشمسي لعطارد يتغير مع كل دورة يدورها الكوكب حول الشمس (الشكل 2-12 (ب)). أطلق على هذا بدارية الحضيض. وكان من السهل تفسير أغلب هذه الحركة على أساس قوى الجذب التي تمارسها الكواكب الأخرى في المجموعة الشمسية. ومع ذلك، لوحظ منذ عام 1845 أن معدل البدارية كان يختلف عن المعدل المتوقع بمقدار 43 ثانية قوسية في القرن. إنه مقدار ضئيل لا شك، لكنه كان موجودًا، وكان يثير القلق نظرًا لعدم وجود تفسير له. إلا أن نظرية أينشتاين فسرته؛ إذ تطلبت النسبية العامة وجود مثل هذه البدارية. وقد أعلن أينشتاين لاحقا أنه عند سماعه بأنباء التحقق من صحة تنبؤه «طار عقله من فرط النشوة لأيام.»

وفي عام 1947، اكتشف جوزيف تايلور وتلميذه راسل هالس أن النجم النابض 1913+16 PSR جزء من نظام نجمي ثنائي. كان النجم النابض (وهو نوع من النجوم المنهارة) يدور في مدار عجيب للغاية حول نجم آخر حول مركز كتلتهما المشتركة، بحيث يقترب كلاهما من الآخر إلى مسافة 1.1 نصف قطر شمسي عند أدنى اقتراب لهما، ثم يتراجعان حتى نصف قطر شمسي قدره 4.8 عند أقصى ابتعاد لهما. وكما تنبأت النسبية العامة، وجد أن الحضيض كان يتقدم بمقدار 4.2 درجات قوسية كل عام؛ أي إن مقدار التقدم في يوم واحد يعادل مقدار التقدم في حركة عطارد في قرن كامل.

اقترح اختبار آخر مثير للاهتمام لأول مرة في عام 1964 من جانب إروين شابيرو، وتضمن استخدام جهاز رادار قوي ونبضات رادار مرتدة من أحد الكواكب. كانت فكرته تقضي بقياس الوقت الذي استغرقته النبضات في الذهاب إلى الكوكب والرجوع منه؛ ومن ثم تتبع مسار الكوكب على نحو دقيق. ثم كررت العملية بينما كان الكوكب على وشك المرور خلف الشمس (انظر الشكل 2-(13. وبناءً على قياسات سابقة، حين كان الكوكب في مواضع مختلفة من السماء، يمكن بسهولة حساب القراءة المتوقعة بينما تمس نبضات الرادار حافة الشمس في الواقع، تبين أن ثمة تأخيرًا زمنيًّا قدره نحو 250 ميكروثانية؛ إذ تسبب مرور النبضات قرب الشمس في إبطائها،

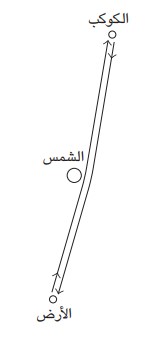
شكل 2-13: اختبار للنسبية العامة مبني على التأخير الزمني لنبضات الرادار المرتدة من أحد الكواكب بينما تمس النبضات حافة الشمس.

وهذا ما تنبأت به نظرية أينشتاين. أُجريت التجربة باستخدام نبضات مرتدة عن كوكبي عطارد والزهرة، باستخدام هذين الكوكبين كعاكسات عملاقة. أُجريت التجربة أيضًا بالاستعانة بالأقمار الصناعية للمسبارات: مارينر 6 و 7 ، فويجر 2 ، وفايكنج مارس لاندر، ومسبار المركبة كاسيني المرسلة إلى زحل في الحالات الأخيرة، استخدمت الأقمار الصناعية في إعادة بث نبضات الرادار أجري أحدث هذه التجارب في عام 2003 باستخدام المسبار كاسيني، وقد تمكن من إثبات صحة التنبؤ وصولاً إلى دقة قدرها جزء واحد في كل 10^-5 أجزاء. لاحظ أن التأثير الذي نتحدث عنه هنا يتضمن قياسات زمنية؛ ومن ثم فهو دليل على أن الزمكان - وليس الفضاء المكان وحده - هو الذي ينحني قرب الأجسام ذات الجاذبية.

نقطة أخيرة تستحق الذكر؛ رأينا في مختلف التجارب التي أُجريت لاختبار النسبية العامة (الانزياح الأحمر الجذبوي، انحناء الضوء، عدسة الجاذبية، تقصي نبضات الرادار بالقرب من الشمس، بدارية حضيض عطارد) أننا كنا نبحث عن تأثريات صغيرة؛ انحرافات طفيفة عما هو متوقع وفقا لقوانين نيوتن للجاذبية. حيث أن هذا يجب ألا يغرينا بالاعتقاد بأن النسبية العامة معنية فقط بالتفاصيل الدقيقة التافهة. فالنسبية العامة تفسر «كل» التأثريات الجذبوية، بما فيها تلك التي يمكن أن تتناولها قوانين نيوتن؛ ومن ثَم، لا تفسر النسبية بدارية حضيض مدار عطارد وحسب، بل تفسر أيضا سبب بقاء عطارد وجميع الكواكب الأخرى في مداراتها من الأساس