
 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 26-8-2021
Date: 29-11-2021
Date: 24-11-2021
|

The traveling salesman problem is a problem in graph theory requiring the most efficient (i.e., least total distance) Hamiltonian cycle a salesman can take through each of 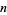 cities. No general method of solution is known, and the problem is NP-hard.
cities. No general method of solution is known, and the problem is NP-hard.
The Wolfram Language command FindShortestTour[g] attempts to find a shortest tour, which is a Hamiltonian cycle (with initial vertex repeated at the end) for a Hamiltonian graph 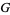 if it returns a list with first element equal to the vertex count of
if it returns a list with first element equal to the vertex count of 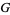 .
.
The traveling salesman problem is mentioned by the character Larry Fleinhardt in the Season 2 episode "Rampage" (2006) of the television crime drama NUMB3RS.
REFERENCES:
Applegate, D.; Bixby, R.; Chvatal, V.; and Cook, W. "Finding Cuts in the TSP (a Preliminary Report)." Technical Report 95-05, DIMACS. Piscataway NJ: Rutgers University, 1995.
Applegate, D.; Bixby, R.; Chvatal, V.; and Cook, W. "Solving Traveling Salesman Problems." http://www.tsp.gatech.edu/.
Hoffman, P. The Man Who Loved Only Numbers: The Story of Paul Erdős and the Search for Mathematical Truth. New York: Hyperion, pp. 168-169, 1998.
Kruskal, J. B. "On the Shortest Spanning Subtree of a Graph and the Traveling Salesman Problem." Proc. Amer. Math. Soc. 7, 48-50, 1956.
Lawler, E.; Lenstra, J.; Rinnooy Kan, A.; and Shmoys, D. The Traveling Salesman Problem: A Guided Tour of Combinatorial Optimization. New York: Wiley, 1985.
Lin, S. "Computer Solutions of the Traveling Salesman Problem." Bell System Tech. J. 44, 2245-2269, 1965.
Platzman, L. K. and Bartholdi, J. J. "Spacefilling Curves and the Planar Travelling Salesman Problem." J. Assoc. Comput. Mach. 46, 719-737, 1989.
Reinelt, G. "TSPLIB--A Traveling Salesman Problem Library." ORSA J. Comput. 3, 376-384, 1991.
Rosenkrantz, D. J.; Stearns, R. E.; and Lewis, P. M. "An Analysis of Several Heuristics for the Traveling Salesman Problem." SIAM J. Comput. 6, 563-581, 1977.
Skiena, S. "Traveling Salesman Tours." §5.3.5 in Implementing Discrete Mathematics: Combinatorics and Graph Theory with Mathematica. Reading, MA: Addison-Wesley, pp. 199-202, 1990.
Skiena, S. S. "Traveling Salesman Problem." §8.5.4 in The Algorithm Design Manual. New York: Springer-Verlag, pp. 319-322, 1997.
Steinhaus, H. Mathematical Snapshots, 3rd ed. New York: Dover, pp. 120-121, 1999.



|
|
|
|
لخفض ضغط الدم.. دراسة تحدد "تمارين مهمة"
|
|
|
|
|
|
|
طال انتظارها.. ميزة جديدة من "واتساب" تعزز الخصوصية
|
|
|
|
|
|
|
عوائل الشهداء: العتبة العباسية المقدسة سبّاقة في استذكار شهداء العراق عبر فعالياتها وأنشطتها المختلفة
|
|
|