المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Kolmogorov Entropy |
 1173
 05:01 مساءً
date: 31-8-2021 |
Author : Ott, E 
Book or Source : Chaos in Dynamical Systems. New York: Cambridge University Press 
Page and Part : ...|
Read More
Date: 15-9-2021
1470
Date: 2-10-2021
1425
Date: 15-10-2021
929
|
Also known as metric entropy. Divide phase space into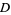 
-dimensional hypercubes of content 
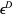. Let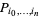 
be the probability that a trajectory is in hypercube 
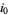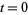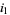at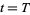 
, 
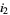at 
, 
at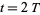 
, etc. Then define
 |
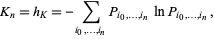(1) |
where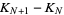 
is the information needed to predict which hypercube the trajectory will be in at 
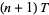given trajectories up to 
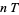. The Kolmogorov entropy is then defined by
 |
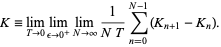(2) |
The Kolmogorov entropy is related to Lyapunov characteristic exponents by
 |
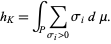(3) |
REFERENCES:
Ott, E. Chaos in Dynamical Systems. New York: Cambridge University Press, p. 138, 1993.
Schuster, H. G. Deterministic Chaos: An Introduction, 3rd ed. New York: Wiley, p. 112, 1995.
|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
العتبة العباسية المقدسة تستعد لإطلاق الحفل المركزي لتخرج طلبة الجامعات العراقية
|
|
|
