
Vector Space
 المؤلف:
Arfken, G
المؤلف:
Arfken, G
 المصدر:
Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press
المصدر:
Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press
 الجزء والصفحة:
pp. 530-534
الجزء والصفحة:
pp. 530-534
 7-8-2021
7-8-2021
 2424
2424
Vector Space
A vector space 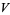 is a set that is closed under finite vector addition and scalar multiplication. The basic example is
is a set that is closed under finite vector addition and scalar multiplication. The basic example is 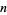 -dimensional Euclidean space
-dimensional Euclidean space 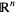 , where every element is represented by a list of
, where every element is represented by a list of 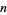 real numbers, scalars are real numbers, addition is componentwise, and scalar multiplication is multiplication on each term separately.
real numbers, scalars are real numbers, addition is componentwise, and scalar multiplication is multiplication on each term separately.
For a general vector space, the scalars are members of a field 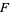 , in which case
, in which case 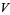 is called a vector space over
is called a vector space over 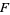 .
.
Euclidean 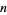 -space
-space 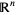 is called a real vector space, and
is called a real vector space, and 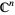 is called a complex vector space.
is called a complex vector space.
In order for 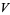 to be a vector space, the following conditions must hold for all elements
to be a vector space, the following conditions must hold for all elements 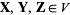 and any scalars
and any scalars 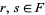 :
:
1. Commutativity:
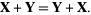 |
(1)
|
2. Associativity of vector addition:
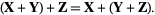 |
(2)
|
3. Additive identity: For all 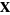 ,
,
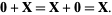 |
(3)
|
4. Existence of additive inverse: For any 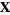 , there exists a
, there exists a 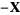 such that
such that
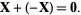 |
(4)
|
5. Associativity of scalar multiplication:
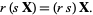 |
(5)
|
6. Distributivity of scalar sums:
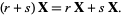 |
(6)
|
7. Distributivity of vector sums:
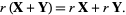 |
(7)
|
8. Scalar multiplication identity:
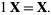 |
(8)
|
Let 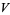 be a vector space of dimension
be a vector space of dimension 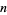 over the field of
over the field of 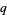 elements (where
elements (where 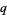 is necessarily a power of a prime number). Then the number of distinct nonsingular linear operators on
is necessarily a power of a prime number). Then the number of distinct nonsingular linear operators on 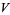 is
is
and the number of distinct 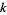 -dimensional subspaces of
-dimensional subspaces of 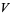 is
is
where 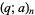 is a q-Pochhammer symbol.
is a q-Pochhammer symbol.
A consequence of the axiom of choice is that every vector space has a vector basis.
A module is abstractly similar to a vector space, but it uses a ring to define coefficients instead of the field used for vector spaces. Modules have coefficients in much more general algebraic objects.
REFERENCES:
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 530-534, 1985.
 الاكثر قراءة في التبلوجيا
الاكثر قراءة في التبلوجيا
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


