
Quotient Vector Space
 المؤلف:
المرجع الالكتروني للمعلوماتيه
المؤلف:
المرجع الالكتروني للمعلوماتيه
 المصدر:
www.almerja.com
المصدر:
www.almerja.com
 الجزء والصفحة:
...
الجزء والصفحة:
...
 4-8-2021
4-8-2021
 1892
1892
Quotient Vector Space
Suppose that ![V=<span style=]() {(x_1,x_2,x_3)}" src="https://mathworld.wolfram.com/images/equations/QuotientVectorSpace/Inline1.gif" style="height:15px; width:100px" /> and
{(x_1,x_2,x_3)}" src="https://mathworld.wolfram.com/images/equations/QuotientVectorSpace/Inline1.gif" style="height:15px; width:100px" /> and ![W=<span style=]() {(x_1,0,0)}" src="https://mathworld.wolfram.com/images/equations/QuotientVectorSpace/Inline2.gif" style="height:15px; width:91px" />. Then the quotient space
{(x_1,0,0)}" src="https://mathworld.wolfram.com/images/equations/QuotientVectorSpace/Inline2.gif" style="height:15px; width:91px" />. Then the quotient space 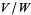 (read as "
(read as "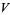 mod
mod 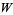 ") is isomorphic to
") is isomorphic to ![<span style=]() {(x_2,x_3)}=R^2" src="https://mathworld.wolfram.com/images/equations/QuotientVectorSpace/Inline6.gif" style="height:17px; width:85px" />.
{(x_2,x_3)}=R^2" src="https://mathworld.wolfram.com/images/equations/QuotientVectorSpace/Inline6.gif" style="height:17px; width:85px" />.
In general, when 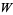 is a subspace of a vector space
is a subspace of a vector space 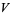 , the quotient space
, the quotient space 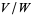 is the set of equivalence classes
is the set of equivalence classes ![[v]](https://mathworld.wolfram.com/images/equations/QuotientVectorSpace/Inline10.gif) where
where 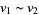 if
if 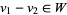 . By "
. By "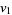 is equivalent to
is equivalent to 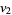 modulo
modulo 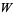 ," it is meant that
," it is meant that 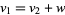 for some
for some 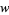 in
in 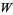 , and is another way to say
, and is another way to say 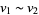 . In particular, the elements of
. In particular, the elements of 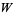 represent
represent ![[0]](https://mathworld.wolfram.com/images/equations/QuotientVectorSpace/Inline21.gif) . Sometimes the equivalence classes
. Sometimes the equivalence classes ![[v]](https://mathworld.wolfram.com/images/equations/QuotientVectorSpace/Inline22.gif) are written as cosets
are written as cosets 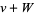 .
.
The quotient space is an abstract vector space, not necessarily isomorphic to a subspace of 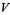 . However, if
. However, if 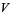 has an inner product, then
has an inner product, then 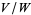 is isomorphic to
is isomorphic to
![W^_|_=<span style=]() {v:<v,w>=0 for all w in W}. " src="https://mathworld.wolfram.com/images/equations/QuotientVectorSpace/NumberedEquation1.gif" style="height:15px; width:201px" /> {v:<v,w>=0 for all w in W}. " src="https://mathworld.wolfram.com/images/equations/QuotientVectorSpace/NumberedEquation1.gif" style="height:15px; width:201px" /> |
In the example above, ![W^_|_=<span style=]() {(0,x_2,x_3)}" src="https://mathworld.wolfram.com/images/equations/QuotientVectorSpace/Inline27.gif" style="height:15px; width:105px" />.
{(0,x_2,x_3)}" src="https://mathworld.wolfram.com/images/equations/QuotientVectorSpace/Inline27.gif" style="height:15px; width:105px" />.
Unfortunately, a different choice of inner product can change 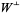 . Also, in the infinite-dimensional case, it is necessary for
. Also, in the infinite-dimensional case, it is necessary for 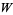 to be a closed subspace to realize the isomorphism between
to be a closed subspace to realize the isomorphism between 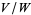 and
and 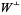 , as well as to ensure the quotient space is a T2-space.
, as well as to ensure the quotient space is a T2-space.
 الاكثر قراءة في التبلوجيا
الاكثر قراءة في التبلوجيا
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


